Geseran melingkar

Dalam matematika kombinatorika, geseran melingkar (bahasa Inggris: circular shift) adalah operasi penataan daftar dalam daftar berurut (tuple) yang menggeser entri terakhir ke awal lalu sisanya mengikuti (tergeser) atau sebaliknya. Geseran melingkar adalah jenis permutasi siklis yang khusus. Secara formal, geseran melingkar adalah permutasi σ dari n entri dalam daftar berurut sehingga

${\displaystyle \sigma (i)\equiv (i+1)}$ modulus n untuk semua entri i = 1, ..., n

atau

${\displaystyle \sigma (i)\equiv (i-1)}$ modulus n untuk semua entri i = 1, ..., n.

Hasil dari penerapan geseran melingkar pada suatu daftar berurut disebut pergeseran melingkar dari daftar berurut tersebut.

Misalnya, penerapan geseran melingkar untuk daftar berurut (a, b, c, d) berturut-turut menghasilkan

• (d, a, b, c),
• (c, d, a, b),
• (b, c, d, a),
• (a, b, c, d) (daftar berurut asli),

dan kemudian berulang; daftar berurut ini memiliki empat pergeseran melingkar yang berbeda. Namun, tidak semua daftar berurut jumlah n memiliki n pergeseran yang berbeda. Misalnya, daftar berurut (a, b, a, b) hanya memiliki dua pergeseran melingkar yang berbeda. Pada umumnya, jumlah pergeseran melingkar dari daftar berurut jumlah n dapat bernilai faktor-faktor n dan bergantung pada entri-entri dalam daftar berurut.

Dalam pemrograman, suatu rotasi tingkat bit, juga dikenal sebagai pergeseran melingkar, adalah operasi tingkat bit yang menggeser semua bitnya. Hal ini berbeda dengan pergeseran aritmetika. Pergeseran melingkar tidak memedulikan bit tanda bilangan atau membedakan pangkat dengan bilangan pokok dalam bilangan titik mengambang. Hal ini juga berbeda dengan pergeseran logika. Posisi bit yang kosong diisi oleh bit yang tergeser keluar dari barisannya.

Geseran melingkar sering dipakai dalam kriptografi untuk melakukan permutasi barisan bit. Sayangnya, meski hampir semua prosesor memiliki instruksi untuk itu (misalnya, Intel x86 memiliki perintah ROL dan ROR), banyak bahasa pemrograman, termasuk C, tidak memiliki operator atau fungsi baku untuk pergeseran melingkar. Namun, beberapa kompilator menerjemahkan kode yang melakukan hal yang sama ke instruksi geseran melingkar yang sesuai. Kebanyakan kompilator C mengenali polanya dan menerjemahkan ke instruksi tunggal.^{[1][catatan 1]}

/*
 * Operasi geseran dalam C hanya didefinisikan untuk jumlah geseran
 * yang nonnegatif dan lebih kecil daripada sizeof(nilai) * CHAR_BIT.
 * Maskernya, yang dipakai dalam operasi AND (&), mencegah perilaku
 * tak terdefinisi ketika jumlah geseran 0 atau lebih besar daripada
 * lebar unsigned int.
 */

#include <stdint.h>  // untuk uint32_t, untuk memakai rotasi 32 bit tanpa memandang ukuran int
#include <limits.h>  // untuk CHAR_BIT

uint32_t rotl32(uint32_t nilai, unsigned int jumlah) {
    const unsigned int masker = CHAR_BIT * sizeof(nilai) - 1;
    jumlah &= masker;
    return (nilai << jumlah) | (nilai >> (-jumlah & masker));
}

uint32_t rotr32(uint32_t nilai, unsigned int jumlah) {
    const unsigned int masker = CHAR_BIT * sizeof(nilai) - 1;
    jumlah &= masker;
    return (nilai >> jumlah) | (nilai << (-jumlah & masker));
}

Implementasi yang aman dan ramah kompilator di atas dikembangkan oleh John Regehr^[3] dan dirapikan lebih lanjut oleh Peter Cordes.^[4][5]

Bentuk yang lebih sederhana biasa ditemui ketika jumlah dibatasi dari 1 sampai 31 bit.

uint32_t rotl32(uint32_t nilai, unsigned int jumlah) {
    return nilai << jumlah | nilai >> (32 - jumlah);
}

Bentuk tersebut cukup berbahaya karena ia akan menggeser sebanyak 32 bit bila jumlah bernilai 0 atau 32 yang tidak didefinisikan dalam bahasa C. Namun, hal ini biasanya tetap bisa dipakai karena kebanyakan mikroprosesor menafsirkan nilai >> 32 sebagai geseran 32 bit (menghasilkan nol) atau tanpa pergeseran dan keduanya menghasilkan nilai yang tepat untuk penggunaan ini.

Untuk C++, penggunaan templat dapat memperluas dukungan untuk semua jenis bilangan bulat.

#include <climits>
// https://stackoverflow.com/a/776550/3770260
template <typename INT>
#if __cplusplus > 201100L // Pakai constexpr dalam C++ 11 untuk mempermudah pengoptimalan
constexpr
#endif // Lihat pula https://stackoverflow.com/a/7269693/3770260
INT rol(INT nilai, size_t jumlah) {
#if __cplusplus > 201100L && _wp_force_unsigned_rotate // Pakai pemeriksaan tak bertanda C++ 11 agar masuk akal
    static_assert(std::is_unsigned<INT>::value,
                  "Geseran kiri hanya masuk akal untuk jenis bilangan bulat tak bertanda");
#endif
    return (nilai << jumlah) | ((unsigned) nilai >> (-jumlah & (sizeof(INT) * CHAR_BIT - 1)));
}

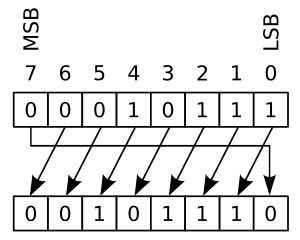
Bila barisan bit 0001 0111 digeser melingkar sebanyak satu bit, barisan tersebut akan menjadi berikut: (lihat gambar)

Apabila geseran melingkar diteruskan, hasil pergeserannya adalah sebagai berikut:

1. ^ Kode ini mendukung instruksi rotate pada CellSPU.^[2]