Himpunan cembung

Dalam geometri, himpunan bagian dari suatu ruang Euklides (atau, lebih umumnya, ruang afin atas lapangan bilangan riil) dikatakan cembung jika untuk setiap dua titik anggota himpunan bagian, maka ruas garis yang menghubungkan kedua titik tersebut terletak sepenuhnya di dalam himpunan bagian tersebut. Dapat juga dikatakan, himpunan cembung atau daerah cembung adalah himpunan bagian yang mengiris setiap garis menjadi suatu ruas garis tunggal (mungkin kosong).^[1][2] Misal, kubus padat adalah himpunan cembung, tetapi apa pun yang berongga atau memiliki lekukan, misalnya, bentuk bulan sabit, bukan cembung.

Himpunan ${\displaystyle {\mathcal {K}}^{2}}$ dari semua benda cembung planar dapat menjadi parameter dalam bentuk diameter tubuh cembung ${\displaystyle D}$, jari-jari lingkaran dalam ${\displaystyle r}$ (lingkaran terbesar yang terkandung dalam tubuh cembung) dan jari-jari lingkaran luar ${\displaystyle R}$ (lingkaran terkecil berisi badan cembung). Bahkan, himpunan ini dapat dijelaskan oleh himpunan ketidaksetaraan yang diberikan oleh ^[3][4]

${\displaystyle {\begin{aligned}2r&\leq D\leq 2R\\R&\leq {\frac {\sqrt {3}}{3}}D\\r+R&\leq D\\D^{2}{\sqrt {4R^{2}-D^{2}}}&\leq 2R(2R+{\sqrt {4R^{2}-D^{2}}})\end{aligned}}}$

dan dapat divisualisasikan sebagai gambar dari fungsi ${\displaystyle g}$ yang memetakan tubuh cembung ke titik ${\displaystyle \mathbb {R} ^{2}}$ yang diberikan oleh ${\textstyle \left({\frac {r}{R}},{\frac {D}{2R}}\right)}$. Gambar fungsi ini dikenal sebagai ${\displaystyle (r,D,R)}$ diagram Blachke-Santaló.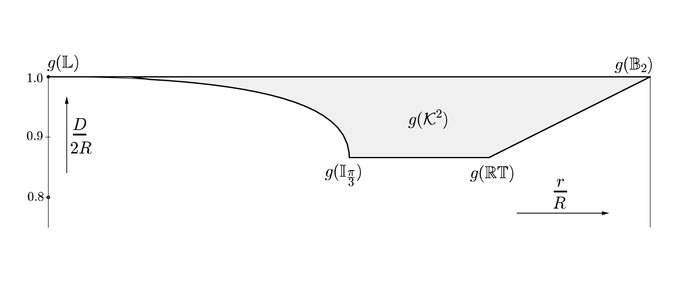

Atau, himpunan ${\displaystyle {\mathcal {K}}^{2}}$ juga dapat diukur dengan lebarnya (jarak terkecil antara dua hiperbidang paralel yang berbeda), perimeter dan luas.^[3][4]

Misalkan C menjadi badan cembung di pesawat. Kita dapat menuliskan ${\displaystyle r}$ persegi panjang di ${\displaystyle C}$ sehingga salinan homothetik ${\displaystyle R}$ dari ${\displaystyle r}$ dibatasi sekitar ${\displaystyle C}$. Rasio homothety positif paling banyak 2 dan:^[5]

${\displaystyle {\tfrac {1}{2}}\cdot \operatorname {Area} (R)\leq \operatorname {Area} (C)\leq 2\cdot \operatorname {Area} (r)}$

Lihat entri himpunan cembung di kamus bebas Wiktionary.

• Hazewinkel, Michiel, ed. (2001) [1994], "Convex subset", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4 
• Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.

Artikel bertopik matematika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya.

• l
• b
• s