قيمة مطلقة

دالة القيمة المطلقة
مخطط بياني يوضح دالة القيمة المطلقة للاعداد الحقيقية.
تدوين	${\displaystyle |x|}$
تعريف الدالة	${\displaystyle |x|={\begin{cases}x,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x<0\end{cases}}}$
مشتق الدالة	${\displaystyle \operatorname {sgn}(x)={\frac {|x|}{x}}={\frac {x}{|x|}}}$ (دالة الإشارة)
مشتق عكسي (تكامل)	${\displaystyle {\frac {x|x|}{2}}}$
الميزات الأساسية
زوجية أم فردية؟	زوجية
مجال الدالة	${\displaystyle \mathbb {R} }$
المجال المقابل	${\displaystyle \mathbb {R} _{+}}$
قيم محددة
القيمة/النهاية عند الصفر	0
نهاية الدالة عند +∞	${\displaystyle +\infty }$
نهاية الدالة عند -∞	${\displaystyle +\infty }$
الحدود الأدنى	0
القيمة/النهاية عند 1	1
القيمة/النهاية عند -1	1
جذور الدالة	0
تعديل مصدري - تعديل

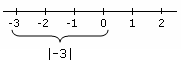القيمة المطلقة^[1] (بالإنجليزية: Absolute Value)‏ هي دالة رياضية تخضع للمواصفات الثلاثة التالية:

• إذا كان ${\displaystyle ||u||}$ يساوي صفرا فإنه حتما ${\displaystyle u=0}$ أي أنه في حالة ${\displaystyle u\neq 0}$ فإن${\displaystyle ||u||}$ أكبر من صفر
• ${\displaystyle ||\lambda u||=|\lambda |.||u||}$
• ${\displaystyle ||u_{1}+u_{2}||\leq ||u_{1}||+||u_{2}||}$

و على هذا الأساس يمكن بناء العديد من الدالات يمكن اعتبارها كلها قيما مطلقة إذا استوفت الشروط المذكورة أعلاه. ولعل أشهر هذه القيم المطلقة القيمة المطلقة الإقليدية. وفي كل الأحوال تعبر القيمة المطلقة عن طول أو مسافة بين الكائنات الرياضية.

بدأ استخدام مصطلح القيمة المطلقة في القرن التاسع عشر، أما الرمز فقد أدخله عالم الرياضيات الألماني كارل فايرشتراس عام 1841.

لأي عدد حقيقي a، يرمز للقيمة المطلقة بالرمز | a | وتعرف ب:

${\displaystyle |a|={\begin{cases}a,&{\mbox{if }}a\geq 0\\-a,&{\mbox{if }}a<0.\end{cases}}}$

من التعريف يتضح أن القيمة المطلقة تكون دائما إما موجبة أو مساوية للصفر ولكن لا يمكن أن تكون سالبة.

من وجهة نظر الهندسة التحليلية فإن القيمة المطلقة هي المسافة من الصفر على طول خط الأعداد الحقيقية. وبتعبير آخر، المسافة بين عددين هي القيمة المطلقة للفرق بينهما.

القيمة المطلقة لعدد صحيح ما، هي المسافة بين ذلك العدد والصفر. وتكون القيمة المطلقة عددا موجبا لِأن المسافات معدودة والأعداد الموجبة هي أعداد العد. يوضع العدد المراد معرفة قيمته المطلقة بين عارضتين أفقيتين | |. الجدول التالى يوضح القيمة المطلقة للأعداد الصحيحة.^[2]

يمكن إعادة تعريف القيمة المطلقة لعدد مركب رياضيا من العلاقة

${\displaystyle |a|={\sqrt {a^{2}}}}$

والذي يمكن تعميمه كما يلي:

لاي عدد مركب

${\displaystyle z=x+iy,\,}$

حيث x وy أعداد حقيقية، القيمة المطلقة لـ z ورمزها |z| تعرف بـ:

${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}.}$

دالة القيمة المطلقة عند عدد حقيقي تعطي قيمته بدون النظر إلى إشارته بينما دالة الإشارة تعطي إشارته دون النظر إلى قيمته. فيما يلي العلاقة التي تربط الدالتين:

${\displaystyle |x|=x\operatorname {sgn}(x),}$

وحين يكون x ≠ 0،

${\displaystyle \operatorname {sgn}(x)={\frac {|x|}{x}}.}$

المسافة الإقليدية الرسمية بين نقطتين

${\displaystyle a=(a_{1},a_{2},\dots ,a_{n})}$

و

${\displaystyle b=(b_{1},b_{2},\dots ,b_{n})}$

في الفضاء الإقليدي ذي البعد n تُعرف كما يلي :

${\displaystyle {\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

يمكن إنشاء دالة القيمة المطلقة باستخدام إحدى لغات البرمجة مثل بيسك أو باسكال أو سي أو اسمبلي أو غيرها بالشروط التالية: مطلق(z)

• إذا كان z أكبر أو يساوي من صفر أرجع z.
• إذا كان z أقل من صفر أرجع -.z

تتميز لغة الجافا سكربت المستخدمة في صفحات الويب بسهولة البرمجة فيها (خاصة لمن يعملون بلغة سي وسي++) ودعم اللغات في إعادة تعريف الدوال وبالتالي يمكن تعريف دالة كما يلي:

function abs(z)
{
   return z < 0 ? -z : z;
}

مطلق = abs;

وتستدعى في البرنامج مثلاً: (abs(-6.7، فتكون النتيجة 6.7.

تعريف القيمة المطلقة على الأعداد الحقيقية يمكن أن يمدد إلى أي حلقة مرتبة. فعلا، إذا كان a عنصرا من الحلقة المرتبة R، فإن القيمة المطلقة ل a والتي يُرمز إليها ب |a| تعرف كما يلي:

${\displaystyle |a|={\begin{cases}a,&{\mbox{if }}a\geq 0\\-a,&{\mbox{if }}a\leq 0\end{cases}}\;}$

حيث a- هو المعاكس الجمعي ل a، و0 هو العنصر المحايد بالنسبة إلى الجمع.

• متوسط القيمة المقومة
• المرونة السعرية للطلب