|
Curtosi En la teoria de la probabilitat i estadística, la curtosi, del grec: κυρτός, kirtós; (corba) convexa, és la mesura de la forma i el grau d'apuntament d'una distribució de probabilitat. En altres paraules, la curtosi mesura si la distribució és apuntada o és aplanada posant el focus en la forma de les cues laterals.[1][2] Per una mateixa variància, com més alta sigui la curtosi d'una distribució significarà que una part més gran dels successos s'esdevenen prop la mitjana i a les cues (cues més gruixudes). La curtosi és el quart moment estandarditzat, definit com: on μ és la mitjana i σ és la desviació estàndard.[3] Sovint es fa servir, en comptes de la curtosi, l'excés de curtosi, que és la diferència entre la curtosi d'una distribució i la de la distribució normal, que és 3.[4][5] En alguns contextos s'anomena curtosi l'excés de curtosi, cosa que pot portar a situacions ambigües. Un distribució amb coeficient de curtosi al voltant del de la normal (excés de curtosi proper a 0) s'anomena mesocúrtica; una amb un excés de curtosi negatiu indica un pic baix i unes cues amples que aviat s'aprimen als costats, s'anomena platicúrtica; una amb excés de curtosi positiu indica un apuntament del pic i unes cues llargues i gruixudes i s'anomena leptocúrtica.[6] En finances s'utilitza com a indicador de la volatilitat que presenta la cotització d'un valor financer. Excés de curtosi en distribucions ben conegudes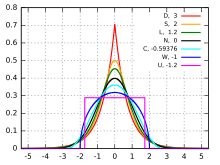 En aquest exemple, comparem diverses distribucions ben conegudes de diferents famílies paramètriques. Totes les densitats considerades aquí són unimodals i simètriques, amb una mitjana i l'asimetria de zero.
Referències
|
![{\textstyle \operatorname {Kurt} [X]=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4d2ad25d648d19d242e0730dd334ebe8cbbaf09)