|
Segment lineal Un segment és el conjunt de punts de l'espai que formen dos punts diferents (A i B), anomenats extrems del segment i tots aquells punts de la recta que passa per A i B que estan situats entremig d'aquests dos punts.[1][2] La recta que conté el segment s'anomena recta suport del segment. Equivalentment, també es pot definir segment com la intersecció entre la semirecta d'origen A i que passa per B amb la semirecta d'origen B i que conté A. El segment se sol representar amb els seus extrems, en aquest cas AB, sovint amb una marca en forma de segment al seu damunt (). Un segment orientat és un vector. Segments consecutius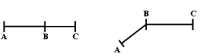 Dos segments són consecutius quan tenen en comú únicament un extrem. Segons tinguin o no la mateixa recta suport, es classifiquen en:[3][4]
La successió de segments consecutius no col·lineals, formen una poligonal, que pot ser oberta o tancada segons si el primer i últim segments tinguin o no extrems comuns. Mètrica dels segmentsEls segments es poden comparar i operar, de manera que es poden considerar quantitats i esdevenen magnitud. ComparacióPostulat de les tres possibilitats (Llei de tricotomia): Donats dos segments, sempre es verifica una de les següents possibilitats i només una:
IgualtatCom en totes les figures es considera que dos segments són iguals (o congruents) si existeix un moviment que pot transformar el primer en el segon. La igualtat de segments compleix les tres propietats de la igualtat entre figures (vegeu figura):
DesigualtatLa desigualtat de segments, compleix amb la propietat transitiva per a les relacions de major i menor. OperacionsSuma La suma de segments està definida per a segments qualssevol, no necessàriament col·lineals, però geomètricament, cal primer obtenir segments iguals als primers (amb un moviment) convertint-los en segments consecutius i col·lineals. La suma de diversos segments consecutius col·lineals dona per resultat un nou segment determinat pels extrems no comuns dels segments considerats.[5] Divisió per un nombre naturalVegeu punt mitjà. Els segments en matemàtiquesEn un espai vectorial (per exemple ℝ² o ℝ3) es pot definir el segment s com:[6] on i són els vectors (per exemple de ℝ² o ℝ3) fixos que representen els extrems del segment i és el vector diferència , que descriu la direcció del segment (o de la recta suport), i el seu mòdul és la longitud del segment. Per altra banda t és un paràmetre real lliure de l'interval . Referències
Vegeu també |

![{\displaystyle s=\{{\vec {A}}+t\cdot {\vec {AB}}\mid t\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76f5b1d5660e1be88cbb9e566abf04832567ccf5)




![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
