|
Algoritmo hill climbingEn ciencia de la computación, el algoritmo hill climbing, también llamado algoritmo de Escalada Simple o ascenso de colinas es una técnica de optimización matemática que pertenece a la familia de los algoritmos de búsqueda local. Es un algoritmo iterativo que comienza con una solución arbitraria a un problema, luego intenta encontrar una mejor solución variando incrementalmente un único elemento de la solución. Si el cambio produce una mejor solución, otro cambio incremental se le realiza a la nueva solución, repitiendo este proceso hasta que no se puedan encontrar mejoras. Suele llamarse a esta búsqueda algoritmo voraz local, porque toma un estado vecino "bueno" sin pensar en la próxima acción. El Algoritmo Hill climbing es interesante para encontrar un óptimo local (una solución que no puede ser mejorada considerando una configuración de la vecindad) pero no garantiza encontrar la mejor solución posible (el óptimo global) de todas las posibles soluciones (el espacio de búsqueda). La característica de que sólo el óptimo local puede ser garantizado puede ser remediada utilizando reinicios (búsqueda local repetida), o esquemas más complejos basados en iteraciones, como búsqueda local iterada, en memoria, como optimización de búsqueda reactiva y búsqueda tabú, o modificaciones estocásticas, como simulated annealing. La relativa simplicidad de este algoritmo lo hace una primera elección popular entre los algoritmos de optimización. Es usado ampliamente en inteligencia artificial, para alcanzar un estado final desde un nodo de inicio. La elección del próximo nodo y del nodo de inicio puede ser variada para obtener una lista de algoritmos de la misma familia. Aunque algoritmos más avanzados tales como simulated annealing o búsqueda tabú pueden devolver mejores resultados, en algunas situaciones hill climbing opera sin diferencias. El hill climbing con frecuencia puede producir un mejor resultado que otros algoritmos cuando la cantidad de tiempo disponible para realizar la búsqueda es limitada, por ejemplo en sistemas en tiempo real. El algoritmo puede devolver una solución válida aún si es interrumpido en cualquier momento antes de que finalice. Por ejemplo, el hill climbing puede ser aplicado al problema del viajante. Es fácil encontrar una solución inicial que visite todas las ciudades pero sería muy pobre comparada con la solución óptima. El algoritmo comienza con dicha solución y realiza pequeñas mejoras a esta, tales como intercambiar el orden en el cual dos ciudades son visitadas. Eventualmente, es probable que se obtenga una ruta más corta. Descripción matemáticaEl hill climbing intenta maximizar (o minimizar) una función objetivo , donde es un vector de valores discretos y/o continuos. En cada iteración, el hill climbing ajustará un único elemento en y determinará si el cambio mejora el valor de . (Note que esto difiere de los métodos de descenso de gradiente, los cuales ajustan todos los valores en en cada iteración de acuerdo al gradiente de la colina.) Con hill climbing, cualquier cambio que mejore es aceptado, y el proceso continúa hasta que no pueda encontrarse un cambio que mejore el valor de . se dice entonces que es "óptima localmente". En los espacios de vectores discretos, cada valor posible para puede ser visualizado como un vértice en un grafo. El hill climbing seguirá el grafo de vértice en vértice, siempre incrementando (o disminuyendo) localmente el valor de , hasta alcanzar un máximo local (o un mínimo local) .  VariantesEn el hill climbing simple, el primer nodo cercano es escogido, mientras que en hill climbing de ascenso pronunciado todos los sucesores son comparados y la solución más cercana es elegida. Ambas formas fallan si no existe un nodo cercano, lo cual sucede si hay máximos locales en el espacio de búsqueda que no son soluciones. El hill climbing de ascenso pronunciado es similar a la búsqueda en anchura, la cual intenta todas las posibles extensiones del camino actual en vez de sólo una. Hill climbing estocástico no examina todos los vecinos antes de decidir cómo moverse. En vez de eso, selecciona un vecino aleatorio, y decide (basado en la cantidad de progreso en ese vecino) si moverse a él o examinar otro. Descenso coordinado realiza una búsqueda en línea a lo largo de una dirección de coordenadas a partir del punto actual en cada iteración. Algunas versiones del descenso coordinado eligen aleatoriamente una dirección coordinada diferente en cada iteración. Hill climbing de reinicio aleatorio es meta-algoritmo construido sobre la base de hill climbing. Es también conocido como Shotgun hill climbing. Este realiza, iterativamente, el hill-climbing, cada vez con una condición inicial aleatoria . La mejor es guardada: si una nueva corrida del hill climbing produce una mejor que el estado guardado, lo reemplaza. Hill climbing de reinicio aleatorio es un algoritmo sorprendentemente efectivo en muchos casos. De esto se deriva que con frecuencia es mejor gastar tiempo de CPU explorando el espacio, que cuidadosamente optimizar desde una condición inicial. ProblemasMáximo local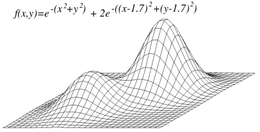 Un problema con el hill climbing es que encontrará sólo el máximo local. A menos que la heurística sea convexa, puede que no alcance el máximo global. Otros algoritmos de búsqueda local tratan de superar este problema, entre ellos hill climbing estocástico, camino aleatorio y simulated annealing.  Cordilleras y corredores (pasadizos)Las cordilleras son un reto para los algoritmos de hill climbing que optimizan en espacios continuos. Debido a que los algoritmos de hill climbing ajustan solo un elemento en el vector a la vez, a cada paso se va a mover en una dirección alineada con el eje. Si la función objetivo determina una cordillera estrecha que asciende en una dirección no alineada con el eje (o si el objetivo es minimizar, un corredor estrecho que desciende en una dirección no alineada con el eje), entonces el algoritmo de hill climbing solo puede ascender la cordillera (o descender por el corredor) en zigzag. Si los lados de la cordillera(o el corredor) son muy pronunciados, entonces el algoritmo puede verse forzado a realizar pasos muy pequeños mientras zigzaguea hacia una mejor posición. De esta manera, puede tomar una cantidad de tiempo irracional ascender la cordillera (o descender el corredor). En cambio, los métodos de descenso del gradiente pueden moverse en cualquier dirección por la cual la cordillera o el corredor pueden ascender o descender. De esta forma, el método de descenso en la dirección del gradiente o método del gradiente conjugado es generalmente preferido sobre hill climbing cuando la función objetivo es diferenciable. Los algoritmos de hill climbing, sin embargo, tienen la ventaja de no requerir que la función objetivo sea diferenciable, por lo que pueden ser preferidos cuando la función es compleja. MesetasOtro problema que a veces ocurre con hill climbing es el de la meseta. Una meseta se encuentra cuando el espacio de búsqueda es plano, o suficientemente plano de manera tal que el valor retornado por la función objetivo es indistinguible de los valores retornados por regiones cercanas debido a la precisión utilizada por la máquina para representar su valor. En estos casos el algoritmo puede que no sea capaz de determinar en qué dirección debe continuar y puede tomar un camino que nunca conlleve a una mejoría de la solución. PseudocódigoDiscrete Space Hill Climbing Algorithm
currentNode = startNode;
loop do
L = NEIGHBORS(currentNode);
nextEval = -INF;
nextNode = NULL;
for all x in L
if (EVAL(x) > nextEval)
nextNode = x;
nextEval = EVAL(x);
if nextEval <= EVAL(currentNode)
//Return current node since no better neighbors exist
return currentNode;
currentNode = nextNode;
Continuous Space Hill Climbing Algorithm
currentPoint = initialPoint; // the zero-magnitude vector is common
stepSize = initialStepSizes; // a vector of all 1's is common
acceleration = someAcceleration; // a value such as 1.2 is common
candidate[0] = -acceleration;
candidate[1] = -1 / acceleration;
candidate[2] = 0;
candidate[3] = 1 / acceleration;
candidate[4] = acceleration;
loop do
before = EVAL(currentPoint);
for each element i in currentPoint do
best = -1;
bestScore = -INF;
for j from 0 to 4 // try each of 5 candidate locations
currentPoint[i] = currentPoint[i] + stepSize[i] * candidate[j];
temp = EVAL(currentPoint);
currentPoint[i] = currentPoint[i] - stepSize[i] * candidate[j];
if(temp > bestScore)
bestScore = temp;
best = j;
if candidate[best] is not 0
currentPoint[i] = currentPoint[i] + stepSize[i] * candidate[best];
stepSize[i] = stepSize[i] * candidate[best]; // accelerate
if (EVAL(currentPoint) - before) < epsilon
return currentPoint;
Comparar algoritmo genético; optimización aleatoria. Véase tambiénEnlaces externos
|



