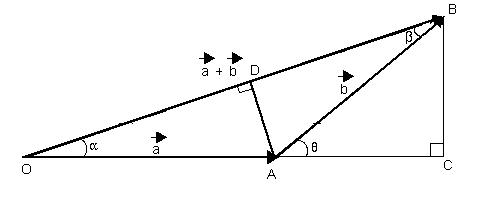
Este artículo presenta una deducción para la expresión del módulo resultante de dos vectores (véase vector (física) y módulo (vector) ) de un espacio vectorial (sobre los números reales ).
Sean dos vectores
a
→
{\displaystyle {\vec {a}}}
b
→
{\displaystyle {\vec {b}}}
θ
{\displaystyle \theta }
Imagen de vectores colocados La fórmula para calcular
|
a
→
+
b
→
|
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|}
Teorema de Pitágoras . En el triángulo OCB:
OB
¯
2
=
OC
¯
2
+
CB
¯
2
{\displaystyle {\overline {\text{OB}}}^{2}={\overline {\text{OC}}}^{2}+{\overline {\text{CB}}}^{2}}
OB
¯
=
|
a
→
+
b
→
|
{\displaystyle {\overline {\text{OB}}}=|{\vec {a}}+{\vec {b}}|}
OC
¯
=
|
a
→
|
+
A
C
{\displaystyle {\overline {\text{OC}}}=\left|{\vec {a}}\left|+AC\right.\right.}
Resultando:
|
a
→
+
b
→
|
2
=
(
|
a
→
|
+
AC
¯
)
2
+
CB
¯
2
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=\left(|{\vec {a}}|+{\overline {\text{AC}}}\right)^{2}+{\overline {\text{CB}}}^{2}}
En el triángulo ACB :
AC
¯
=
|
b
→
|
cos
θ
{\displaystyle {\overline {\text{AC}}}=|{\vec {b}}|\cos \theta }
CB
¯
=
|
b
→
|
sin
θ
{\displaystyle {\overline {\text{CB}}}=|{\vec {b}}|\sin \theta }
Sustituyendo esto en la igualdad de antes resulta:
|
a
→
+
b
→
|
2
=
(
|
a
→
|
+
|
b
→
|
cos
θ
)
2
+
(
|
b
→
|
sin
θ
)
2
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=\left(|{\vec {a}}|+|{\vec {b}}|\cos \theta \right)^{2}+\left(|{\vec {b}}|\sin \theta \right)^{2}}
|
a
→
+
b
→
|
2
=
|
a
→
|
2
+
2
|
a
→
|
|
b
→
|
cos
θ
+
|
b
→
|
2
cos
2
θ
+
|
b
→
|
2
sin
2
θ
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}|\cos \theta +|{\vec {b}}|^{2}\cos ^{2}\theta +|{\vec {b}}|^{2}\sin ^{2}\theta }
|
a
→
+
b
→
|
2
=
|
a
→
|
2
+
2
|
a
→
|
|
b
→
|
cos
θ
+
|
b
→
|
2
(
cos
2
θ
+
sin
2
θ
)
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|^{2}=|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}|\cos \theta +|{\vec {b}}|^{2}\left(\cos ^{2}\theta +\sin ^{2}\theta \right)}
cos
2
θ
+
sin
2
θ
=
1
⇒
|
a
→
+
b
→
|
2
=
|
a
→
|
2
+
2
|
a
→
|
|
b
→
|
cos
θ
+
|
b
→
|
2
{\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1\quad \Rightarrow \quad \left|{\vec {a}}+{\vec {b}}\right|^{2}=|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}|\cos \theta +|{\vec {b}}|^{2}}
|
a
→
+
b
→
|
=
|
a
→
|
2
+
2
|
a
→
|
|
b
→
|
cos
θ
+
|
b
→
|
2
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|={\sqrt {|{\vec {a}}|^{2}+2|{\vec {a}}||{\vec {b}}|\cos \theta +|{\vec {b}}|^{2}}}}
|
a
→
+
b
→
|
=
|
a
→
|
2
+
|
b
→
|
2
+
2
|
a
→
|
|
b
→
|
cos
θ
{\displaystyle \left|{\vec {a}}+{\vec {b}}\right|={\sqrt {|{\vec {a}}|^{2}+|{\vec {b}}|^{2}+2|{\vec {a}}||{\vec {b}}|\cos \theta }}}