|
Nodo (física) Un nodo es un punto estacionario donde la onda tiene una amplitud (física) mínima. Por ejemplo, en una cuerda vibrante como la de una guitarra, los extremos de la cuerda son nodos. Al cambiar la posición del nodo final pulsando un traste, el guitarrista cambia la longitud efectiva de la cuerda vibrante y, por lo tanto, la nota producida. El opuesto de un nodo es un antinodo, un punto donde la amplitud de la onda estacionaria es máxima. Estos puntos se sitúan a mitad de camino entre los nodos.[1]Y también son parte de la física Explicación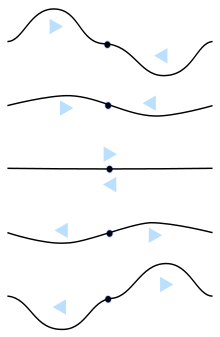 Una onda estacionaria se produce cuando dos trenes de ondas sinusoidales de la misma frecuencia se mueven en direcciones opuestas en el mismo espacio e interfieren entre sí.[2] Se forman cuando las ondas se reflejan en un límite físico, como el sonido reflejado desde una pared o la radiación electromagnética reflejada desde el final de una línea de transmisión, y particularmente cuando las ondas están confinadas en un oscilador en resonancia, rebotando hacia adelante y hacia atrás entre dos límites, como en un tubo de órgano o una cuerda de un instrumento musical. En una onda estacionaria, los nodos son una serie de ubicaciones a intervalos igualmente espaciados donde la amplitud de la onda (y, por lo tanto, su movimiento) es cero (véase la animación anterior). En estos puntos, las dos ondas se suman con fases opuestas y se anulan mutuamente. Se localizan a intervalos separados por la mitad de una longitud de onda (λ / 2). A mitad de camino entre cada par de nodos se presentan ubicaciones donde la amplitud es máxima. Estos puntos se llaman antinodos. En estos puntos, las dos ondas se suman con la misma fase y se refuerzan mutuamente. En los casos en que los dos trenes de onda opuestos no tienen la misma amplitud, no se cancelan a la perfección, por lo que la amplitud de la onda estacionaria en los nodos no es cero, sino simplemente un mínimo. Esto ocurre cuando el reflejo en el límite es imperfecto, lo que se indica mediante una razón de onda estacionaria finita, la relación entre la amplitud de la onda en el antinodo y la amplitud en el nodo. En la resonancia de una superficie bidimensional o membrana, como un parche de tambor o placa de metal vibrante, los nodos se convierten en líneas nodales, líneas en la superficie donde la superficie está inmóvil, dividiendo la superficie en regiones separadas que vibran con la fase opuesta. Estos pueden hacerse visibles rociando arena en la superficie, y los intrincados patrones de líneas resultantes se llaman patrones de Ernst Chladni. En líneas de transmisión de corriente alterna, un nodo de voltaje es un antinodo de intensidad y un antinodo de voltaje es un nodo de intensidad. Los nodos son los puntos de desplazamiento cero, no los puntos donde se cruzan dos ondas constituyentes. Condiciones de fronteraLa posición de los nodos en relación con el límite que refleja las ondas depende de las condiciones finales, o lo que es lo mismo, se trata de un problema de condición de frontera. Aunque hay muchos tipos de condiciones finales, los extremos de los resonadores suelen ser uno de los dos tipos que provocan una reflexión total:
Ejemplos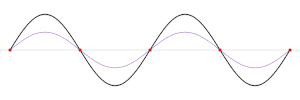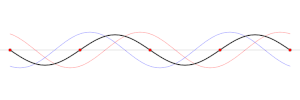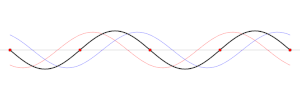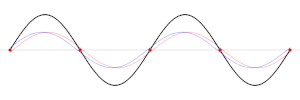 SonidoUna onda de sonido consiste en ciclos alternados de compresión y expansión del medio de onda. Durante la compresión, las moléculas del medio se fuerzan a juntarse, lo que se traduce en una mayor presión y densidad. Durante la expansión, las moléculas se separan, lo que produce la disminución de la presión y la densidad. La cantidad de nodos en una longitud especificada es directamente proporcional a la frecuencia de la onda. Ocasionalmente, en una guitarra, violín u otro instrumento de cuerda, los nodos se usan para crear armónicos. Cuando el dedo se coloca en la parte superior de la cuerda en cierto punto, pero no se lleva hasta el traste, se crea un tercer nodo (adicional a los formados en el puente y en la cejilla) y se emite un armónico. Durante la interpretación normal, cuando se usan los trastes, los armónicos están siempre presentes, aunque son menos sonoros. Con el método de nodo artificial, el sobretono es más fuerte y el tono fundamental es más tenue. Si el dedo se coloca en el punto medio de la cuerda, se escucha el primer sobretono, que está una octava por encima de la nota fundamental que se tocaría, si el armónico no suene. Cuando dos nodos adicionales dividen la cuerda en tercios, esto crea una octava y un quinto perfecto (duodécimo). Cuando tres nodos adicionales dividen la cuerda en cuartos, esto crea una doble octava. Cuando cuatro nodos adicionales dividen la cuerda en quintas, esto crea una octava doble y una tercera mayor (17.ª). La octava, el tercio principal y el quinto perfecto son las tres notas presentes en un acorde mayor. El sonido característico que permite al oyente identificar un instrumento en particular se debe en gran parte a la magnitud relativa de los armónicos creados por el instrumento. QuímicaEn química, las ondas u «orbitales» según la mecánica cuántica, se usan para describir las propiedades ondulatorias de los electrones. Muchas de estas ondas cuánticas también tienen nodos y antinodos. El número y la posición de estos nodos y antinodos dan lugar a muchas de las propiedades de un átomo o enlace covalente. Los orbitales atómicos se clasifican según el número de nodos radiales y angulares, mientras que los orbitales moleculares se clasifican de acuerdo con el carácter de vinculación. Los orbitales moleculares con un antinodo entre los núcleos son muy estables y se conocen como «orbitales de unión» que fortalecen el vínculo. En contraste, los orbitales moleculares con un nodo entre los núcleos no serán estables debido a la repulsión electrostática y se conocen como «orbitales antiadherentes», que debilitan el enlace. Otro concepto de mecánica cuántica es el de partícula en una caja, donde el número de nodos de la función de onda puede ayudar a determinar el estado de energía cuántica: los nodos cero corresponden al estado fundamental, un nodo corresponde al primer estado excitado, etc. En general,[3] organiza los autoestados en el orden de las energías crecientes, , las funciones propias también caen en el orden de un número creciente de nodos; la enésima función propia tiene n-1 nodos, entre cada uno de los cuales las siguientes funciones propias tienen al menos un nodo. Referencias
|
