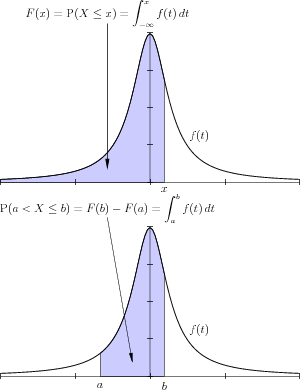
Diagrammissa on jatkuvan satunnaismuuttujan kuvaaja, johon on väritetty näkyviin tapahtuman "todennäköisyysmassat". Väritetyn alueen määrätty integraalit eli kuvaajan pinta-alat ovat suhteessa tapahtuman todennäköisyyteen.Kertymäfunktio [ 1] jakaumafunktio [ 2] engl. cumulative distribution function cdf ) on todennäköisyyslaskennassa ja tilastotieteessä reaaliarvoisen satunnaismuuttujan todennäköisyyden jakautumista kuvaava funktio. Kertymäfunktion
F
(
x
)
{\displaystyle F(x)}
tapahtumissa , jossa satunnaismuuttuja
X
{\displaystyle X}
x
{\displaystyle x}
F
(
x
)
=
P
(
X
≤
x
)
{\displaystyle \scriptstyle F(x)=P(X\leq x)}
Jatkuvan satunnaismuuttujan tapauksessa kertymäfunktio määritellään tiheysfunktion määrätyn integraalin avulla ja diskreetillä satunnaismuuttujalla pistetodennäköisyyksien summana . Kertymäfunktio on aina oikealta jatkuva , vaikka tiheysfunktio tai pistetodennäköisyysfunktio olisi epäjatkuva.[ 1] [ 2] [ 3]
Diskreetin satunnaismuuttujan kertymäfunktio määritellään
F
(
x
)
=
P
(
X
≤
x
)
=
∑
k
≤
x
p
(
k
)
,
{\displaystyle F(x)=P(X\leq x)=\sum _{k\leq x}p(k),}
[ 2] [ 3] missä
p
(
k
)
{\displaystyle p(k)}
x
{\displaystyle x}
[ 3]
Jatkuvan satunnaismuuttujan kertymäfunktio määritellään määrättynä integraalina ylärajan
x
{\displaystyle x}
F
(
x
)
=
P
(
X
≤
x
)
=
∫
−
∞
x
f
(
t
)
d
t
,
{\displaystyle F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)dt,}
[ 1] [ 3] missä
f
(
x
)
{\displaystyle f(x)}
F
(
a
)
{\displaystyle F(a)}
a
{\displaystyle a}
[ 4] [ 3]
Jos tiheysfunktio on jatkuva, saadaan se myös derivoimalla kertymäfunktio muuttujan suhteen
F
′
(
x
)
=
f
(
x
)
.
{\displaystyle F'(x)=f(x).}
[ 1]
Jos halutaan korostaa kertymäfunktion satunnaismuuttujaa, merkitään satunnaismuuttuja usein alaindeksiksi
F
X
(
x
)
{\displaystyle F_{X}(x)}
F
Y
(
x
)
.
{\displaystyle F_{Y}(x).}
kreikkalaisella aakkosella
Φ
(
x
)
{\displaystyle \Phi (x)}
ϕ
(
x
)
{\displaystyle \phi (x)}
[ 4]
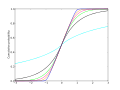
Ylin kuvaaja esittää diskreetin satunnaismuuttujan kertymäfunktiota, keskimmäinen jatkuvan satunnaismuuttujan ja alin sellaisen satunnaismuuttujan, jolla on kumpaakin piirrettä.
Diskreetti satunnaismuuttuja
Diskreetin satunnaismuuttujan pistetodennäköisyysfunktiolla saa 10 nollasta eroavaa arvoa
P
(
X
=
x
i
)
=
p
(
x
i
)
=
f
(
x
i
)
,
{\displaystyle P(X=x_{i})=p(x_{i})=f(x_{i}),}
kun
i
=
1
,
.
.
.
,
10
,
{\displaystyle i=1,...,10,}
p
(
x
i
)
=
1
10
.
{\displaystyle p(x_{i})={\tfrac {1}{10}}.}
x pienempien kohtien todennäköisyyksien summasta eli
F
(
x
)
=
P
(
X
≤
x
)
=
∑
x
i
≤
x
p
i
=
p
1
+
p
2
+
.
.
.
+
p
k
.
{\displaystyle F(x)=P(X\leq x)=\sum _{x_{i}\leq x}p_{i}=p_{1}+p_{2}+...+p_{k}.}
[ 5] [ 1] Tämän porrasfunktion arvot ovat oikealta jatkuvia ja sen kuvaaja on esitetty alla.
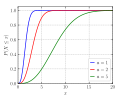
Jatkuva satunnaismuuttuja
Tasaisen jakauman tiheysfunktio välillä [a,b] on [ 6]
f
(
x
)
=
{
1
b
−
a
,
jos
x
∈
[
a
,
b
]
0
,
jos
x
∉
[
a
,
b
]
{\displaystyle f(x)={\begin{cases}{\frac {1}{b-a}},&{\mbox{jos }}x\in [a,b]\\0,&{\mbox{jos }}x\notin [a,b]\end{cases}}}
[ 1] ja sen kertymäfunktioksi saadaan
F
(
x
)
=
∫
−
∞
x
f
(
t
)
d
t
=
{
0
,
jos
x
<
a
x
−
a
b
−
a
,
jos
x
∈
[
a
,
b
]
1
,
jos
x
>
b
.
{\displaystyle F(x)=\int _{-\infty }^{x}f(t)dt={\begin{cases}0,&{\mbox{jos }}x<a\\{\frac {x-a}{b-a}},&{\mbox{jos }}x\in [a,b]\\1,&{\mbox{jos }}x>b.\end{cases}}}
[ 1] Sen kuvaaja on alla.
Ominaisuuksia
Funktiona
Kertymäfunktio on kuvaus reaaliluvuilta välille
[
0
,
1
]
{\displaystyle [0,1]}
F
(
x
)
:
R
→
[
0
,
1
]
.
{\displaystyle F(x):\mathbb {R} \rightarrow [0,1].}
[ 3] Jatkuvan satunnaismuuttujan kertymäfunktio on jatkuva funktio. Diskreetin satunnaismuuttujan kertymäfunktio on oikealta jatkuva porrasfunktio.[ 2]
P
(
X
<
a
)
=
lim
x
→
a
F
(
x
)
=
lim
x
→
a
P
(
X
<
x
)
=
P
(
X
≤
a
)
=
F
(
a
)
.
{\displaystyle P(X<a)=\lim _{x\to a}F(x)=\lim _{x\to a}P(X<x)=P(X\leq a)=F(a).}
Tämä ominaisuus voidaan kirjoittaa havainnollisemmin
P
(
X
≤
a
)
=
P
(
X
<
a
tai
X
=
a
)
=
P
(
X
<
a
)
+
P
(
X
=
a
)
=
P
(
X
<
a
)
.
{\displaystyle P(X\leq a)=P(X<a{\mbox{ tai }}X=a)=P(X<a)+P(X=a)=P(X<a).}
[ 4] Jatkuvan satunnaismuuttujan pistetodennäköisyys eli arvo yksittäisessä pisteessä on siten nolla eli
P
(
X
=
a
)
=
0.
{\displaystyle P(X=a)=0.}
Koska kertymäfunktion arvot ovat tapahtumien todennäköisyyksiä, saa se vain arvoja väliltä
0
≤
F
(
x
)
≤
1.
{\displaystyle 0\leq F(x)\leq 1.}
[ 1] [ 3] Kertymäfunktio on lisäksi monotoninen funktio , joka on ei-vähenevä eli
F
(
x
1
)
≤
F
(
x
2
)
{\displaystyle F(x_{1})\leq F(x_{2})}
x
1
<
x
2
{\displaystyle x_{1}<x_{2}}
[ 1] [ 3] Tämän vuoksi kertymäfunktio kasvaa lopulta täyteen arvoonsa, kun ylärajaa kasvatetaan riittävästi
lim
a
→
+
∞
F
(
a
)
=
lim
a
→
+
∞
∫
−
∞
a
f
(
x
)
d
x
=
1.
{\displaystyle \lim _{a\to +\infty }F(a)=\lim _{a\to +\infty }\int _{-\infty }^{a}f(x)\,dx=1.}
[ 3] Kertymäfunktio alkaa nollasta jostakin arvosta a lähtien. Jos satunnaismuuttuja arvoalue on äärettömän laaja, voidaan tämä ilmaista
lim
a
→
−
∞
F
(
a
)
=
lim
a
→
−
∞
∫
−
∞
a
f
(
x
)
d
x
=
0.
{\displaystyle \lim _{a\to -\infty }F(a)=\lim _{a\to -\infty }\int _{-\infty }^{a}f(x)\,dx=0.}
[ 3]
Edellä esitelty määritelmä on eräs tapa ilmaista tapahtuma , jossa todennäköisyys lasketaan käyttämällä satunnaismuuttujan ylärajana
x
{\displaystyle x}
P
(
X
≤
x
)
=
F
(
x
)
.
{\displaystyle P(X\leq x)=F(x).}
Voidaan osoittaa, että sillä voidaan laskea kaikki sellaiset todennäköisyydet, jossa tapahtumat ovat välejä. Esimerkiksi, koska mielivaltaiselle satunnaismuuttujan arvolle
a
{\displaystyle a}
P
(
X
<
a
)
+
P
(
a
≤
X
)
=
1
,
{\displaystyle P(X<a)+P(a\leq X)=1,}
[ 4] voidaan vastatapahtuman todennäköisyys laskea
P
(
a
≤
X
)
=
1
−
P
(
X
<
a
)
=
1
−
P
(
X
≤
a
)
=
1
−
F
(
a
)
.
{\displaystyle P(a\leq X)=1-P(X<a)=1-P(X\leq a)=1-F(a).}
[ 3] Toisaalta, koska mielivaltaisille satunnaismuuttujan arvoille
a
{\displaystyle a}
b
{\displaystyle b}
P
(
X
<
a
)
+
P
(
a
≤
X
≤
b
)
=
P
(
X
≤
b
)
,
{\displaystyle P(X<a)+P(a\leq X\leq b)=P(X\leq b),}
[ 4] voidaan välin
[
a
,
b
]
{\displaystyle [a,b]}
laskea
P
(
a
≤
X
≤
b
)
=
P
(
X
≤
b
)
−
P
(
X
<
a
)
=
P
(
X
≤
b
)
−
P
(
X
≤
a
)
=
F
(
b
)
−
F
(
a
)
.
{\displaystyle P(a\leq X\leq b)=P(X\leq b)-P(X<a)=P(X\leq b)-P(X\leq a)=F(b)-F(a).}
[ 3] Jos kertymäfunktio olisi määritelty toisella tavalla, olisi siihenkin voitu johtaa kaikkien muidenkin välien todennäköisyydet.
↑ a b c d e f g h i Kivelä, Simo K.: Kertymäfunktio , M niin kuin matematiikka, 10.8.2000
↑ a b c d Ruskeapää, Heikki: Todennäköisyyslaskenta I (luentomoniste), Turun Yliopisto, 2012
↑ a b c d e f g h i j k l Melin, Ilkka: Kertymäfunktio , Todennäköisyyslaskennan kurssimateriaali, Aalto-yliopisto, 2007
↑ a b c d e Alatupa, Sami et al.: Pitkä Sigma 3 , s. 154−164. (lukion pitkän matematiikan oppikirja) Helsinki: Tammi, 2010. ISBN 978-951-31-5343-4 ↑ Alatupa, Sami et al.: Pitkä Sigma 3 , s. 43−60. (lukion pitkän matematiikan oppikirja) Helsinki: Tammi, 2010. ISBN 978-951-31-5343-4 ↑ Mathworld: Uniform Distribution




















![{\displaystyle f(x)={\begin{cases}{\frac {1}{b-a}},&{\mbox{jos }}x\in [a,b]\\0,&{\mbox{jos }}x\notin [a,b]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d78e5ff6b10166d14c8fa0b6c9de570d7b70218)
![{\displaystyle F(x)=\int _{-\infty }^{x}f(t)dt={\begin{cases}0,&{\mbox{jos }}x<a\\{\frac {x-a}{b-a}},&{\mbox{jos }}x\in [a,b]\\1,&{\mbox{jos }}x>b.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29720bc3ee32b42fe36ffc2e12f7635d7a6be877)










![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle F(x):\mathbb {R} \rightarrow [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bf5078c52044611ac0163fb432464b08a9a5fe3)













![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)




