|
Pression atmosphérique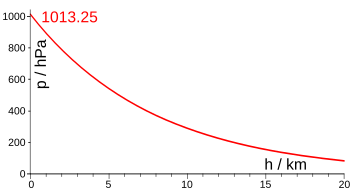 Formule du nivellement barométrique : .  La pression atmosphérique est la pression de l'air (sur Terre) ou plus généralement du mélange gazeux constituant l'atmosphère considérée. Cette pression se traduit par une force exercée sur toute surface en contact avec elle, perpendiculaire à la surface et d'intensité proportionnelle à son aire. C'est la gravité qui comprime l'atmosphère, de telle sorte qu'à chaque niveau la pression locale supporte le poids de la colonne d'air sus-jacente. Cette pression dépend donc de l'altitude, mais elle dépend aussi des conditions atmosphériques (circulation atmosphérique globale et vents locaux) en accord avec le théorème de Bernoulli. La pression atmosphérique au niveau de la mer est en moyenne de 1,013 25 × 105 Pa (ou 1 013,25 hPa), soit 1,013 25 bar ou 1 atm par définition de cette dernière unité. La pression atmosphérique se mesure à l'aide d'un baromètre, d'un hypsomètre ou d'un altimètre. Elle a été longtemps exprimée en mmHg (millimètres de mercure) en raison de l'emploi courant du baromètre à colonne de mercure. Depuis l'adoption du pascal dans le Système international d'unités (SI) comme unité de la pression, les météorologues utilisent un multiple de cette unité, l'hectopascal (hPa), qui a l'avantage de correspondre exactement au millibar utilisé auparavant : 1 hPa = 1 mbar. Historique En 1638, Galilée écrit Discours et démonstrations mathématiques concernant deux nouvelles sciences, où il décrit diverses expériences, dont une conçue par Aristote qui permet de mettre en évidence le poids de l'air grâce à une bouteille contenant l'air comprimé[2]. Dans son ouvrage, le savant rapporte une observation que les fontainiers de Florence lui ont soumise sur l'impuissance où se trouvent les pompes aspirantes des fontaines à soulever l’eau au-dessus de 10 mètres. Galilée attribue cette impuissance à une cause intrinsèque, l'horreur limitée du vide, en reprenant l'idée aristotélicienne fausse de l'horror vacui (« la nature a horreur du vide »). En 1643, Torricelli, ami et disciple de Galilée, réalise une expérience (en) qui lui permet d'attribuer l'élévation de l'eau à une cause extérieure, la pression atmosphérique, et de mesurer précisément le poids de l'atmosphère[3]. Les expériences des hémisphères de Magdebourg réalisées par Otto von Guericke à partir de 1654 montrent que la pression atmosphérique pousse les deux demi-boules l'une contre l'autre à raison de dix tonnes par mètre carré. Pression atmosphérique normaleLa pression atmosphérique réellement mesurée varie autour de la pression atmosphérique normale fixée, par définition[4], comme étant, au « niveau de la mer » (niveau moyen), à la température de 15 °C, de :
Dans les anciennes unités du Système CGS, la pression atmosphérique normale vaut :
Par définition du millimètre de mercure (mmHg) et du torr (Torr) qui lui est égal, la pression atmosphérique normale vaut exactement 760 mmHg = 760 Torr. Enfin la pression atmosphérique normale permet elle-même de définir une unité de pression : 1 atm = 101 325 Pa. À 20 °C, la vitesse moyenne des molécules d'air à pression atmosphérique normale est d'environ 500 m/s (1 800 km/h) ; à 100 °C, cette vitesse d'agitation atteint 560 m/s (2 016 km/h)[5]. Mais à 20 °C et à la pression atmosphérique, la distance moyenne entre les molécules est de l'ordre de dix fois le diamètre de ces molécules et le libre parcours moyen de l'ordre de cent fois ce diamètre. Les molécules s'entrechoquent très souvent (chacune subit en moyenne une collision toutes les 10−10 s), elles ne gardent cette vitesse que sur de très courtes distances)[6]. Variation verticaleLa pression atmosphérique diminue quand l'altitude augmente, car la masse -- et donc le poids -- de l'air sus-jacent diminue nécessairement avec la hauteur, comprimant l'air de moins en moins. La pression diminue, exponentiellement, d'un facteur 10 chaque fois que l'on s'élève de 16 km (ou de moitié à 5 500 m). Il est ainsi possible d'utiliser la pression pour mesurer la hauteur, ce qui est le principe de base de l'altimètre utilisé en aéronautique et en alpinisme. En météorologie appliquée, la pression est souvent utilisée directement comme coordonnée verticale. On parlera par exemple de la température à (une « hauteur » de) 700 hPa. Cette approche a des avantages techniques et elle simplifie certaines équations utilisées en météorologie. Stabilité et instabilitéEn règle générale, la pression atmosphérique diminue de moitié à environ 5 500 mètres et la température moyenne de l'atmosphère diminue de 9,7 °C par 1 000 mètres[7]. Cependant, ce taux n'est valable que pour une atmosphère normalisée et varie en fait selon le contenu en vapeur d'eau et l'altitude. Ces propriétés peuvent être démontrées rigoureusement si l'on fait l'hypothèse que l'atmosphère est en équilibre (bien que cela demeure une excellente approximation, cela n'est pas tout à fait vrai en pratique). Lorsque le sol est chauffé par le Soleil, par convection, les basses couches de l'atmosphère sont réchauffées et comme l'air chaud est moins dense, l'air réchauffé va avoir tendance à s'élever grâce à la poussée d'Archimède. Si la poche d'air chaud se refroidit moins vite que l'air environnant, cette parcelle d'air va accélérer vers le haut. On est alors en présence d'une masse d'air instable. Dans le cas contraire, l'air en ascension devient plus froid que l'air environnant, le mouvement ascendant va s'interrompre et l'atmosphère est alors stable. Le taux de refroidissement de la masse d'air en ascension peut être calculé théoriquement, ou sur un diagramme thermodynamique, par rapport à la température de l'environnement donnée par un radiosondage. Ce calcul repose sur l'hypothèse qu'il n'y a pas d'échange calorique avec l'air extérieur et que le taux de changement de température est différent si l'air est saturé ou pas. Dans le premier cas, la vapeur d'eau condensée est retirée de la masse en ascension. Variation horizontale  Les météorologues analysent les variations horizontales de la pression atmosphérique pour localiser et suivre les systèmes météorologiques : cela permet de définir les zones de dépressions (D) (pression généralement inférieure à 1 013 hPa, 760 mmHg), les zones anticycloniques (A) (pression généralement supérieure à 1 013 hPa, 760 mmHg) et les isobares. Les dépressions et les creux barométriques sont généralement associés au mauvais temps. Les anticyclones et les crêtes barométriques sont quant à eux favorables au beau temps. La différence de pression entre deux points de même altitude (ou gradient horizontal de pression) est également la plus importante force motrice du vent : des valeurs de 5 hPa/km ont été observées dans les cyclones tropicaux les plus violents. Afin d'utiliser la pression pour suivre les systèmes météo et estimer la force du vent, il est nécessaire de faire concorder des mesures de pression qui ont été prises à différentes altitudes : en mer, dans les vallées, en montagne. Pour ce faire, on soumet les mesures brutes de pression à un ajustement standardisé. La valeur résultant de cet ajustement est appelée pression au niveau de la mer, ou PNM. Si l'on prend par exemple le cas d'une station située à 100 mètres au-dessus du niveau de la mer, l'ajustement sera effectué en estimant la pression au fond d'un trou fictif, de 100 mètres de profondeur, qu'on aurait creusé à la station. Plus précisément, la valeur de la PNM est fonction de la pression mesurée à la station et de la température assignée à la colonne d'air fictive. Pour cette dernière on utilise la moyenne de la température actuelle à la station et de celle mesurée douze heures auparavant. La PNM est une approximation d'une grande utilité, mais il faut se garder de lui donner toute la valeur d'une mesure physique exacte, particulièrement en terrain montagneux. La pression atmosphérique mesurée au niveau de la mer varie autour d'une valeur moyenne de 1 013 hPa. La pression mesurée au sol est utilisée pour l'étalonnage et la validation des données en provenance d'instruments météorologiques de mesure à distance. Des mesures précises de pression sont ainsi un fondement nécessaire pour l'observation de la Terre et du climat. Valeurs types
Valeurs records
Observations et expériencesExpérience du verre retourné L'expérience du « verre retourné » ou « verre inversable » consiste à remplir un verre de liquide non gazeux, recouvrir son ouverture d'une feuille de papier cartonné (ou un support équivalent)[15], retourner délicatement le verre puis retirer la main qui maintient le papier. Le liquide reste dans le verre. Cette observation contre-intuitive s'explique de la manière suivante : la pression atmosphérique (environ 1 kg/cm2) et, dans une moindre mesure la tension superficielle, exercent une force verticale ascendante plus importante que le poids du liquide contenu dans le verre et la pression de l'air au fond du verre. Si le support est retiré, le liquide s'échappe bien que la pression atmosphérique exerce la même force ascendante : les forces gravitationnelles (déstabilisantes) prennent le pas sur les forces de tension superficielle (stabilisantes) et déclenchent l'instabilité de Rayleigh-Taylor[16]. Un corollaire de cette expérience est l'ouverture d'un bocal de confiture, de conserve en verre ou de pot de bébé, rendue difficile par la pression atmosphérique supérieure à la pression de l'air extrêmement faible sous le couvercle. Un autre corollaire est « l'eau bouillant sans feu » avec l'ouverture d'un verre sans pied recouvert d'un mouchoir enfoncé dans l'intérieur de façon qu'il soit en contact avec la surface liquide et rabattu extérieurement autour du verre. Une fois le verre renversé, ramener avec une main le mouchoir jusqu'à ce qu'il se trouve bien tendu sur l'ouverture. On entend alors un bouillonnement et on observe de grosses bulles s'élever à travers l'eau agitée comme si elle bouillait. En tendant le mouchoir, on produit un « vide partiel » à l'intérieur du verre, ce qui entraîne l'air extérieur à traverser les pores du tissu et de l'eau pour combler ce « vide »[17]. Expérience de l'ascension de l'eau dans une enceinte où un combustible a brûléLa combustion d'une allumette ou d'une bougie qui repose sur le fond d'un récipient empli d'eau (assiette, cristallisoir …) et qui est placée sous une enceinte (typiquement un verre), met en évidence la pression atmosphérique[18]. La consommation partielle d'oxygène[19] due à la combustion de la cire de paraffine[20] produit du dioxyde de carbone CO2 et de l'eau H2O, deux produits de réaction qui sont sous forme gazeuse. Le refroidissement du gaz résiduel (contraction thermique)[21] et la condensation de la vapeur d'eau (observable par la formation de buée sur les parois internes de l'enceinte) entraînent une diminution de la pression interne qui devient inférieure à la pression atmosphérique externe. Contrairement aux idées reçues parfois enseignées, c'est principalement ce phénomène qui explique que l'eau est poussée vers l'intérieur du verre par la pression atmosphérique[22],[23]. Notes et références
Voir aussiArticles connexes
Liens externes
|



