|
Gradient descent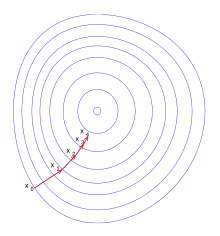 Gradient descent (בתרגום מילולי: מורד הגרדיאנט) היא שיטת אופטימיזציה איטרטיבית מסדר ראשון למציאת מינימום מקומי של פונקציה. בשיטה זו, נעשה צעד נגדי לגרדיאנט ביחס לנקודה הנוכחית. לעומת זאת, אם נעשה צעדים בכיוון של הגרדיאנט נמצא את המקסימום המקומי של הפונקציה (אלגוריתם זה נקרא Gradient ascent, בתרגום מילולי: מעלה הגרדיאנט). מבוא אינטואיטיביהשיטה עובדת על שדה סקלרי של נתונים. שדה סקלרי הוא פונקציה המתאימה לכל נקודה במרחב ערך מספרי. המרחב יכול להיות בעל מספר רב של ממדים. דוגמה לשדה סקלרי בשני ממדים הוא מפה טופוגרפית, בה לכל נקודה על המפה הדו-ממדית משויך הגובה מעל פני הים. לפי השיטה משתמשים בגרדיאנט, שהוא כלי מתמטי וקטורי, כלומר בעל כיוון, המאפשר למצוא את הכיוון אליו הנגזרת מקסימלית דהיינו הכיוון בו נמצא השינוי הדרסטי ביותר בין הנתונים סביב נקודה מסוימת. במפה הטופוגרפית יהווה הגרדיאנט הכיוון בו השיפוע מקסימלי, והאלגוריתם אמור להתכנס למינימום מקומי של השדה הסקלרי . השיטה עובדת כך שבכל שלב של ההפעלה היא מתקדמת לכיוון הפוך לגרדיאנט (כיוון שהגרדיאנט מראה את השיפוע כלפי מעלה) כך שבכל שלב יש התקדמות נגד השיפוע המקסימלי עד שמגיעים לנקודה מספיק נמוכה המוגדרת בתנאי העצירה. דבר זה דומה לאדם העומד בנקודה על המפה הטופוגרפית אך ישנו ערפל סמיך אשר עוצר בעדו. לכן באפשרותו לבדוק רק את סביבתו הקרובה. הכיוון שבו הוא יורד יהיה הכיוון בו המדרון תלול ביותר. תיאור מתמטיGradient descent מבוססת על ההבחנה שאם פונקציה מרובת משתנים מוגדרת ודיפרנציאבילית בסמוך לנקודה , אז יורדת בצורה התלולה ביותר כשהולכים מ בכיוון נגדי לגרדיאנט של ב-, . מכאן שאם עבור קטן דיו, אז . במילים אחרות, הביטוי מוחסר מ- כיוון שרוצים לזוז נגד כיוון הגרדיאנט, מטה לכיוון המינימום. בהתבסס על הבחנה זו, ניתן לנחש נקודה ראשונית כנקודת מינימום של , ולקבל את הסדרה כך ש: שבהתבסס על ההבחנה: הסדרה יכולה להתכנס לנקודת המינימום המבוקשת. גודל הצעד יכול להשתנות בכל איטרציה. יחד עם הנחות מסוימות על הפונקציה (לדוגמה, קמורה ו ליפשיצית) ובחירות מתאימות של (למשל באמצעות line search שמקיים את תנאי וולף או שיטת ברזילאי-בורווין להלן), מתכנסת הסדרה למינימום מקומי. כאשר הפונקציה היא קמורה, ניתן להשתמש ב-gradient descent למציאת פתרון גלובלי. ב-1964 הציג בוריס תאודורוביץ' פוליאק הרחבה לשיטה שנקראת שיטת המומנטום אשר משפרת את קצב ההתכנסות.[1] ב-1983 הציג יורי נסטרוב את שיטת הגרדיאנט המואץ (Nesterov’s Accelerated Gradient ולעיתים בקיצור NAG), שיכולה להשיג קצב התכנסות טוב יותר.[2] גרסה נוספת של Gradient descent מבוססת על הערכה סטוכסטית של הגרדיאנט וידועה כ-Stochastic gradient descent. אלגוריתםלהלן קוד פייתון של האלגוריתם gradient descent: # x0 - initial guess
# df - gradient of function
def gradient_descent(x0, df):
cur_x = x0 # The algorithm starts at x0
gamma = 0.01 # step size multiplier
precision = 0.00001
previous_step_size = cur_x
while previous_step_size > precision:
prev_x = cur_x
cur_x += -gamma * df(prev_x)
previous_step_size = abs(cur_x - prev_x)
return cur_x
קישורים חיצונייםהערות שוליים
|














![{\displaystyle \gamma _{n}={\frac {(\mathbf {x} _{n}-\mathbf {x} _{n-1})^{T}[\nabla F(\mathbf {x} _{n})-\nabla F(\mathbf {x} _{n-1})]}{||\nabla F(\mathbf {x} _{n})-\nabla F(\mathbf {x} _{n-1})||^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eee32f1ea2756daeff530a5828d6d481bae75d8f)