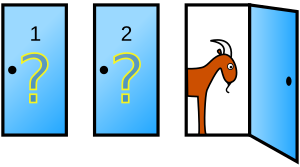
Problema di Monty Hall

Il problema di Monty Hall (o paradosso di Monty Hall) è un famoso problema di teoria della probabilità, legato al gioco a premi statunitense Let's Make a Deal. Prende il nome da quello del conduttore dello show, Monty Hall. Il problema è anche noto come paradosso di Monty Hall, poiché la soluzione può apparire controintuitiva, ma non si tratta di una vera antinomia, in quanto non genera contraddizioni logiche.

Nel gioco vengono mostrate al concorrente tre porte chiuse; dietro ad una si trova un'automobile, mentre ciascuna delle altre due nasconde una capra. Il giocatore può scegliere una delle tre porte, vincendo il premio corrispondente. Dopo che il giocatore ha selezionato una porta, ma non l'ha ancora aperta, il conduttore dello show – che conosce ciò che si trova dietro ogni porta – apre una delle altre due, rivelando una delle due capre, e offre al giocatore la possibilità di cambiare la propria scelta iniziale, passando all'unica porta restante; cambiare la porta migliora le chance del giocatore di vincere l'automobile, portandole da 1/3 a 2/3.

Una famosa formulazione del problema è contenuta in una lettera del 1990 di Craig F. Whitaker, indirizzata alla rubrica di Marilyn vos Savant nel settimanale Parade:

Supponi di partecipare a un gioco a premi, in cui puoi scegliere fra tre porte: dietro una di esse c'è un'automobile, dietro le altre, capre. Scegli una porta, diciamo la numero 1, e il conduttore del gioco a premi, che sa cosa si nasconde dietro ciascuna porta, ne apre un'altra, diciamo la 3, rivelando una capra. Quindi ti domanda: "Vorresti scegliere la numero 2?" Ti conviene cambiare la tua scelta originale?

Quella proposta sopra è una formulazione del problema data da Steve Selvin, in una lettera all'American Statistician (febbraio 1975). Così impostato, il problema è in realtà una variazione sul tema del gioco a premi originale; Monty Hall in effetti apriva una porta dietro cui si trovava una capra per aumentare la tensione, ma non consentiva ai giocatori di cambiare la propria scelta originale. Come scrisse lo stesso Monty Hall a Selvin:

E se mai dovesse partecipare al mio gioco, le regole sarebbero le stesse per lei - nessuno scambio dopo la scelta originale.
—(letsmakeadeal.com) Archiviato l'8 aprile 2010 in Internet Archive.

Marilyn vos Savant risolse il problema correttamente; l'episodio fece un certo scalpore, in quanto diversi accademici non riconobbero la correttezza della soluzione proposta da vos Savant finché questa non la spiegò nel dettaglio in un successivo articolo.

La successiva lettera di Selvin all'America Statistician (agosto, 1975) battezza il problema come "Problema di Monty Hall".

Un problema essenzialmente identico appare in ogni modo nella rubrica Mathematical Games (sulla rivista Scientific American) di Martin Gardner nel 1959, col nome di "Problema dei tre prigionieri".^[1][2]

Questo problema era stato ideato dal matematico francese Joseph Louis François Bertrand che lo aveva proposto nel suo libro Calcul des Probabilités (1889) ed era noto come il Paradosso delle tre scatole di Bertrand.

Quella che segue, per concludere, è una formulazione del problema priva di ambiguità, con vincoli espliciti concernenti il comportamento del conduttore, presentata da Mueser e Granberg:

• Dietro ciascuna di tre porte c'è un'automobile o una capra (due capre, un'automobile in tutto); la probabilità che l'automobile si trovi dietro una data porta è identica per tutte le porte;
• Il giocatore sceglie una delle porte; il suo contenuto non è rivelato;
• Il conduttore sa ciò che si nasconde dietro ciascuna porta;
• Il conduttore deve aprire una delle porte non selezionate, e deve offrire al giocatore la possibilità di cambiare la sua scelta;
• Il conduttore aprirà sempre una porta che nasconde una capra;
  • Cioè, se il giocatore ha scelto una porta che nasconde una capra, il conduttore aprirà la porta che nasconde l'altra capra;
  • Se invece il giocatore ha scelto la porta che nasconde l'automobile, il conduttore sceglie a caso una delle due porte rimanenti;
• Il conduttore offre al giocatore la possibilità di reclamare ciò che si trova dietro la porta che ha scelto originalmente, o di cambiare, reclamando ciò che si trova dietro la porta rimasta.

Le probabilità di vittoria aumentano per il giocatore se cambia la propria scelta?

La risposta è: sì, le probabilità di trovare l'automobile raddoppiano.^[3][4]

La soluzione può essere illustrata come segue. Ci sono tre scenari possibili, ciascuno avente probabilità 1/3:

• Il giocatore sceglie la capra numero 1. Il conduttore sceglie l'altra capra, la numero 2. Cambiando, il giocatore vince l'auto.
• Il giocatore sceglie la capra numero 2. Il conduttore sceglie l'altra capra, la numero 1. Cambiando, il giocatore vince l'auto.
• Il giocatore sceglie l'auto. Il conduttore sceglie una capra, non importa quale. Cambiando, il giocatore trova l'altra capra.

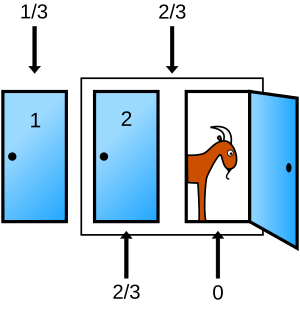
Nei primi due scenari, cambiando il giocatore vince l'auto; nel terzo scenario il giocatore che cambia non vince. Dal momento che la strategia "cambiare" porta alla vittoria in due casi su tre, le chance di vittoria adottando la strategia sono 2/3.

Una spiegazione alternativa è considerare che, se si suppone di cambiare porta, il solo caso in cui si perde è quello in cui originariamente si è scelta l'automobile, che ha probabilità pari a 1/3 e quindi quella di vincere è pari 2/3, dovendo essere la somma delle probabilità di tutti gli eventi pari a uno. Cambiando, il raddoppio delle probabilità di vincere rispetto alla situazione iniziale è dovuto al fatto che avendo il conduttore eliminato una capra ciò garantisce che se il giocatore ha scelto inizialmente l'altra porta con la capra vince essendo rimasta solo la porta con l'auto. Invece, prima della eliminazione di una capra, cambiando avrebbe avuto la probabilità di vincere sempre pari a 1/3.

Il problema sarebbe diverso se non ci fosse una scelta iniziale, o se il conduttore scegliesse una porta a caso, o se il conduttore potesse offrire al giocatore di cambiare a seconda della scelta iniziale del giocatore. Alcune formulazioni del problema, e significativamente quella del settimanale Parade, non escludono esplicitamente queste possibilità; diversi testi di probabilità elementare riportano varianti del problema. Per esempio, se il conduttore offre la possibilità di cambiare solo se il giocatore inizialmente ha scelto l'automobile, le chance di vittoria associate alla strategia "cambiare" sono, ovviamente, dello 0%. Nella formulazione proposta nella sezione precedente, il giocatore che cambia ha una probabilità di vittoria pari a 2/3 precisamente perché il conduttore deve offrirgli la possibilità di cambiare, e deve rivelare una capra.

L'obiezione più comune alla soluzione è fornita dall'idea che, per varie ragioni, il passato possa essere ignorato quando si valutano delle probabilità. Dunque, la scelta della prima porta e il ragionamento del conduttore circa quale porta aprire si possono trascurare; dal momento che si può scegliere tra due porte, la probabilità di scegliere quella giusta dovrebbe essere pari al 50%, indipendentemente che si decida di cambiare o mantenere la porta scelta. In realtà le due porte rimanenti sono diverse perché la prima scelta dal concorrente ha 3 possibili risultati casuali: capra o altra capra o auto; la seconda scelta dal conduttore ha 2 risultati vincolati: auto se il giocatore ha scelto la porta con una capra, capra se il giocatore ha scelto la porta con l'auto. Quindi non possono avere la stessa probabilità. È come se la porta scelta dal conduttore "assorbisse" la probabilità di quella scartata. Perché in effetti, cambiando porta, il giocatore passa effettivamente dal diritto di aprire una porta sola per trovare l'auto, a quella di aprirne due (e quindi ha il doppio di possibilità di vincere); semplicemente le due porte sono aperte per lui dal conduttore che ne scarta una sicuramente perdente e ne lascia una che ha due volte la probabilità, ovverosia il doppio, 2/3 di essere vincente (una possibilità se il giocatore ha scelto la porta con la prima capra e un'altra se il giocatore ha scelto la porta con la seconda capra).

L'errore nel valutare al 50% e 50% è considerare i due eventi, esserci l'auto o non esserci l'auto, come se fossero palline numerate in un sacchetto da cui estrarne una, in cui basta sapere il numero delle palline. Ma solo se gli eventi possibili hanno la stessa probabilità, la probabilità di un evento specifico sarà pari a 1/n, dove n è il numero degli eventi. Si pensi alla probabilità che un pezzo di formaggio in una scatola opaca fuori dal frigo sia ammuffito. Gli eventi possibili sono due, ma la loro probabilità non è 50% e 50%, in realtà la probabilità che sia ammuffito dipende dal tempo.^[5] Nel caso delle porte non il tempo ma l'azione del conduttore, come detto, cambia la probabilità di vincere della porta scelta da lui.

Per confutare l'ipotesi del 50% e 50% possiamo anche porci una domanda. Ipotizziamo che un giocatore adotti la strategia di non accettare mai l'offerta del conduttore, qualunque essa sia. Se le probabilità di vincita all'inizio sono del 33%, ha senso pensare che queste passino automaticamente al 50% solo perché il conduttore ha chiesto qualcosa che il giocatore non ascolta neanche? La risposta è no.

Uno scenario che giustificherebbe la stima del 50% da parte del giocatore sarebbe il seguente: supponiamo che le capre e l'auto vengano collocate da un operatore nascosto non all'inizio del gioco, bensì dopo la scelta (casuale) della porta da parte del conduttore prima però che questa venga effettivamente aperta. L'operatore viene incaricato di simulare il gioco, quindi metterà necessariamente una capra dietro la porta da aprire mentre l'auto e la capra rimasta saranno messe casualmente dietro le restanti due porte. Dopo avere aperto la porta la probabilità di vincere da parte del giocatore diviene effettivamente del 50%.

Sebbene ignorare il passato funzioni in certi giochi, come ad esempio nel lancio di una moneta, non funziona necessariamente in tutti i giochi. Un rilevante controesempio è fornito dal conteggio delle carte uscite in certi giochi di carte, che consente ai giocatori di sfruttare a proprio vantaggio l'informazione riguardante eventi passati. Questo tipo di informazione è utile nella soluzione del problema di Monty Hall, come illustrato negli esempi che seguono.

Infatti, è più facile (probabile) che il giocatore si trovi ad aver scelto (prima scelta nel passato) una capra (aveva due possibilità su tre per una capra contro una possibilità su tre per l'automobile).

Quello che realmente fa la differenza è la conoscenza del futuro o almeno la restrizione dei possibili eventi futuri. Mentre nel lancio della moneta le probabilità di uscita testa o croce non dipendono dai lanci passati, negli esempi di carte (contare le carte) o del problema di Monty Hall i possibili eventi futuri si "riducono" dopo un preciso episodio. Nel caso del contare le carte, l'uscita di una carta modifica le possibili carte che possono ancora uscire, quindi ne modifica la probabilità. Nel caso del problema di Monty Hall, l'esclusione da parte del conduttore di una scelta certamente "sconveniente" rende la porta rimanente più interessante della prima porta scelta quando non si aveva nessuna conoscenza.

In realtà l'errore cognitivo basilare è di considerare la possibilità di scelta offerta dal presentatore al concorrente, dopo aver aperto la porta con la capra, come una giocata diversa, come se il gioco ricominciasse ex novo, e quindi le probabilità si azzerassero rispetto alla prima giocata; in realtà il gioco continua, con le stesse probabilità; al concorrente, dopo la proposta del presentatore, conviene cambiare porta, in quanto, se non la cambiasse, non potrebbe approfittare dell'informazione che gli dà il presentatore aprendo la porta con la capra, porta che il concorrente non ha modo di sapere quale sia prima che il presentatore la apra; nel momento in cui quest'informazione arriva al concorrente, quest'ultimo ha una sola possibilità di approfittarne, cioè cambiare la porta scelta: in questo modo, a fronte del gioco, è come se gli fosse data la possibilità di scegliere 2 porte su 3 per tentare di vincere l'auto, da cui la probabilità di 2/3 (66%). Se non facesse il cambio, rimarrebbe invariabilmente "bloccato" sulla probabilità di 1/3 (33%) della sua giocata iniziale, avvenuta fatalmente prima di avere l'informazione certa di dove si trovasse una delle due capre in gioco.

La probabilità che l'auto sia dietro la porta restante può essere calcolata con l'ausilio del diagramma di Venn illustrato sotto. Dopo aver scelto la porta 1, per esempio, il giocatore ha probabilità 1/3 di aver selezionato la porta con l'auto, il che assegna una probabilità pari a 2/3 alle due porte restanti. Si osservi che c'è una probabilità pari a 1 di trovare una capra dietro almeno una delle due porte non selezionate dal giocatore, dal momento che c'è una sola auto in palio.

Si supponga che il conduttore apra la porta 3. Dal momento che può solo aprire una porta che nasconde una capra, e non apre una porta a caso, questa informazione non ha effetto sulla probabilità che l'auto sia dietro la porta originariamente selezionata, che resta pari a 1/3. Ma l'auto non è dietro la porta 3, dunque l'intera probabilità di 2/3 delle due porte non selezionate dal giocatore è ora assegnata alla sola porta 2, come mostrato sotto. Un modo alternativo per arrivare a questa conclusione è osservare che se l'auto si trova dietro la porta 2 o dietro la porta 3, aprire la porta 3 implica che l'auto si trova dietro la 2 e viceversa.

Osserviamo che il problema non cambierebbe se il conduttore, anziché aprire una porta, offrisse al giocatore la possibilità di cambiare la porta scelta con entrambe le altre. In questo caso è evidente che la probabilità è 2/3.

Viceversa, la situazione cambierebbe completamente se il presentatore, dopo aver escluso la porta 3, scambiasse casualmente i premi nascosti dietro le porte 1 e 2. In questo caso il giocatore avrebbe probabilità 1/2 di vincere sia se mantiene la porta 1, sia se la cambia. Senza questo rimescolamento le probabilità restano 1/3 e 2/3.

Un'analisi del problema attraverso il teorema di Bayes rende esplicito l'effetto delle ipotesi sopra indicate. Si consideri, senza perdere la generalità dell'analisi, che il concorrente scelga la porta 1 e che il conduttore riveli poi una capra dietro alla porta 3. La questione è allora se convenga rimanere sulla scelta iniziale della porta 1, oppure cambiare alla porta 2.

Il teorema di Bayes ci permette di calcolare rapidamente la probabilità a posteriori che l'automobile si trovi dietro la porta 2:

${\displaystyle P(A2|C3)={\frac {P(C3|A2)P(A2)}{P(C3)}}={\frac {1\times {\frac {1}{3}}}{\frac {1}{2}}}={\frac {2}{3}},}$

poiché la probabilità a priori (utilizzando il gergo della statistica bayesiana) che l'automobile si trovi dietro la porta 2, denotata con ${\displaystyle P(A2)}$, è chiaramente 1/3, in quanto l'auto ha a priori la stessa probabilità di trovarsi dietro ciascuna porta. La probabilità a priori che il conduttore apra la porta 3, ${\displaystyle P(C3)}$, è invece 1/2, visto che il conduttore ha a priori due porte tra cui scegliere per rivelare una delle due capre. A posteriori invece, la probabilità che il conduttore apra la porta 3 per rivelare una capra, posto che l'automobile sia dietro la porta 2, ${\displaystyle P(C3|A2)}$, è uguale a 1, perché, avendo il concorrente già selezionato la porta 1, al conduttore resta la possibilità di aprire solamente la porta 3, visto che, se aprisse la porta 2, rivelerebbe l'automobile.

Nel caso in cui venga invece confermata la scelta iniziale della porta 1, si può calcolare ancora tramite il teorema di Bayes la probabilità di trovare qui l'automobile:

${\displaystyle P(A1|C3)={\frac {P(C3|A1)P(A1)}{P(C3)}}={\frac {{\frac {1}{2}}\times {\frac {1}{3}}}{\frac {1}{2}}}={\frac {1}{3}},}$

poiché ${\displaystyle P(A1)=1/3}$ e ${\displaystyle P(C3)=1/2}$ come nel calcolo precedente, mentre la probabilità a posteriori che il conduttore apra la porta 3, posto che l'auto si trovi dietro la porta 1, ${\displaystyle P(C3|A1)}$, è qui uguale a 1/2, perché, avendo il concorrente scelto inizialmente la porta 1, c'è uguale probabilità che il conduttore scelga la porta 3 come la porta 2 per rivelarvi una capra.

Risulta pertanto dimostrato grazie al teorema di Bayes che la probabilità di trovare l'automobile modificando la scelta iniziale (${\displaystyle P(A2|C3)}$) è doppia rispetto alla probabilità di trovarla confermando la scelta iniziale (${\displaystyle P(A1|C3)}$).

Dimostriamo ora che, cambiando sempre l'ultima scelta, la probabilità di vincere l'automobile è ${\displaystyle {\frac {2}{3}}}$ mediante il teorema delle probabilità totali. Ricordiamo che la nostra strategia è di scegliere mentalmente due porte, di indicare al conduttore l'altra porta e poi di cambiare. Indichiamo con ${\displaystyle V}$ l'evento "vittoria seguendo questa strategia". Sia ${\displaystyle A}$ l'evento "sotto le due porte scelte mentalmente c'è la macchina" e ${\displaystyle B}$ l'evento complementare. Si ha ${\displaystyle P(A)={\frac {2}{3}}}$. Si noti anche che ${\displaystyle P(V|A)=1}$ poiché, grazie alla strategia scelta, se la macchina si trova dietro le due porte scelte mentalmente, il conduttore ci indicherà poi quella vincente aprendo la porta perdente. Per il teorema delle probabilità totali abbiamo allora

${\displaystyle P(V)=P(V|A)P(A)+P(V|B)P(B)=1\times {\frac {2}{3}}+0\times {\frac {1}{3}}={\frac {2}{3}}.}$

Dopo la scelta del concorrente, il conduttore apre una delle due porte rimaste. Poiché non sa cosa c'è dietro, con probabilità 1/3 trova l'auto e il gioco finisce. Con probabilità 2/3 trova invece la capra e può chiedere al concorrente se vuole effettuare il cambio con la porta rimasta chiusa. In questo caso accettare lo scambio non fa aumentare al concorrente la sua probabilità di vincere che a questo punto è di 1/2 qualunque sia la sua decisione.^[6]

Ad alcuni minuti dalla fine del gioco, il conduttore sceglie due concorrenti a cui proporre "la grande scommessa". Dietro a una delle tre porte c'è il premio più consistente. Ad ogni giocatore è permesso scegliere una porta (non la stessa).

In questo scenario, si può esaminare una variante del problema. Il presentatore elimina il giocatore che abbia scelto una porta con dietro la capra (se lo hanno fatto entrambi, ne viene scelto uno a caso), apre la porta, svelando la capra e poi offre al giocatore rimanente la possibilità di cambiare la propria scelta. Il giocatore dovrebbe effettuare lo scambio?

La risposta è no. La ragione: il giocatore che effettuasse lo scambio in questo tipo di gioco vincerebbe se e solo se entrambi i giocatori avessero scelto una porta con la capra. che probabilità ha questa evenienza? 1/3. Se mantenesse la scelta resterebbero 2/3 di probabilità. Quindi chi mantenesse la scelta fatta inizialmente avrebbe il doppio delle possibilità di vincere.

In alternativa, ci sono tre possibili scenari, tutti con uguale probabilità (1/3):

• Il giocatore 1 sceglie la porta che nasconde l'auto. Il conduttore deve eliminare il giocatore 2. Cambiare scelta comporta perdere.
• Il giocatore 2 sceglie la porta che nasconde l'auto. Il conduttore deve eliminare il giocatore 1. Cambiare scelta comporta perdere.
• Nessuno dei giocatori sceglie la porta che nasconde l'auto. Il conduttore elimina a caso uno dei due giocatori. Cambiare scelta comporta vincere.

Il giocatore 1 è l'unico rimasto nel primo caso, e lo è con probabilità 1/2 nel terzo caso; in questa eventualità cambiare scelta comporta una probabilità di perdere (1/3) due volte maggiore di quella di vincere (1/6). Analogamente, nel secondo caso il giocatore 2 è l'unico rimasto, e lo è con probabilità 1/2 nel terzo caso; in questa eventualità cambiare scelta comporta una probabilità di perdere (1/3) due volte maggiore di quella di vincere (1/6). Dunque a prescindere da quale giocatore rimanga, c'è una probabilità pari a 2/3 di vincere se non si cambia scelta. Per rendere più palese la differenza rispetto al caso precedente si può dire che non si può qui ragionare come prima dove il (solo) giocatore arriva sempre al secondo turno (quello del possibile scambio) e la probabilità che abbia selezionato la scelta vincente rimane 1/3, contro i complementari 2/3 della scelta alternativa. Si deve invece notare che nell'istante in cui un giocatore (uno dei due) arriva al secondo turno deve considerare che la probabilità che abbia inizialmente effettuato la scelta giusta si modifica e sale a 2/3. In sostanza il giocatore rimasto riveste in questo caso, in termini di probabilità, lo stesso ruolo che prima (caso con un giocatore) ricopriva la porta non selezionata dal giocatore né eliminata dal conduttore.

Esiste una generalizzazione del problema originale in cui si hanno ${\displaystyle n}$ porte: nel primo stadio del gioco, il giocatore sceglie una porta. Quindi il conduttore apre un'altra porta, che nasconde una capra. Se il giocatore vuole, può quindi cambiare scelta e passare a un'altra porta. Il conduttore aprirà allora un'ulteriore porta, ancora non aperta, che nasconde una capra, diversa da quella attualmente scelta dal giocatore. Il giocatore ha quindi la possibilità di cambiare ancora scelta, e così via. Questo procedimento continua fino a che non restano che due porte non ancora aperte: la scelta corrente del giocatore, e un'altra porta. Quante volte dovrebbe cambiare scelta il giocatore, e a che punto del gioco (sempre che cambi almeno una volta)?

La migliore strategia è: restare con la prima scelta sino a che non rimangano solo due porte e a quel punto cambiare. Seguendo questa strategia la probabilità di vincere è ${\displaystyle (n-1)/n}$. Questa variante del paradosso di Monty Hall si deve a Bapeswara Rao e Rao.

Una comune variante del problema è nota ai giocatori di bridge da ben prima che l'articolo della Vos Savant fosse pubblicato. Tale variante è nota come principio della scelta ristretta.^[7]

Esiste una versione quantistica del paradosso, che illustra alcuni aspetti della relazione tra la teoria dell'informazione classica (non quantistica) e l'informazione quantistica, ossia l'informazione codificata negli stati di sistemi meccanici quantistici. Le tre porte sono rimpiazzate da un sistema quantistico che consta di tre alternative, in cui aprire una porta e vedere cosa nasconde si traduce in fare una particolare misurazione. Le regole del gioco possono essere espresse in questo linguaggio, e ancora una volta il giocatore può scegliere se restare fedele alla propria scelta iniziale o cambiare e optare per una scelta alternativa ("ortogonale"). Quest'ultima strategia ha probabilità di vittoria doppie, esattamente come nel caso classico. Tuttavia, se la posizione del premio non è pienamente casuale in senso quantistico, il giocatore può fare ancora meglio, e in determinati casi vincere con probabilità pari a uno. È disponibile in rete un articolo al riguardo, nonché un'applet che illustra gli effetti così descritti.

Poiché in questo gioco i casi possibili non sono molti, si può pensare di schematizzarli come segue, raggruppandoli seguendo la scelta della porta iniziale:

Scelgo la porta A

1. GGC → (M apre la 2) → GXC → resto-perdo, cambio-vinco

2. GCG → (M apre la 3) → GCX → resto-perdo, cambio-vinco

3. CGG → (M apre la 2 o la 3) → CXG o CGX → resto-vinco, cambio-perdo

Scelgo la porta B

1. GGC → (M apre la 1) → XGC → resto-perdo, cambio-vinco

2. GCG → (M apre la 1 o la 3) → XCG o GCX → resto-vinco, cambio-perdo

3. CGG → (M apre la 3) → CGX → resto-perdo, cambio-vinco

Scelgo la porta C

1. GGC → (M apre la 1 o la 2) → XGC o GXC → resto-vinco, cambio-perdo

2. GCG → (M apre la 1) → XCG → resto-perdo, cambio-vinco

3. CGG → (M apre la 2) → CXG → resto-perdo, cambio-vinco

Le disposizioni in elenco numerate da uno a tre sono le configurazioni in cui si possono trovare disposte le due capre (G=Goat) e l'auto (C=Car) dietro ciascuna porta (A,B o C) all'inizio del gioco. Ovviamente non cambiano al cambiare della prima scelta del concorrente e sono a lui del tutto ignote. Dopo tale scelta iniziale, il conduttore (M=Monty) apre una delle due porte che nascondono le capre, cosicché rimangono due porte chiuse, cioè quella inizialmente scelta e l'ultima da aprire: ad esempio, in caso di scelta della porta A ed in presenza della disposizione 1, avremo il caso iniziale GGC (in cui il grassetto indica la porta scelta), dove Monty sarà costretto a rivelare la capra dietro la porta B, cioè, indicando con X la porta aperta non più in gioco, ci troveremo nel caso GXC. In questo caso, se il concorrente rimane sulla propria scelta iniziale (resto), perde.

Come si può notare semplicemente contando i casi vincenti relativi ad ogni modalità di gioco, cioè qualsiasi porta inizialmente lui scelga e considerando le tre disposizioni possibili, ne esistono due su tre favorevoli al concorrente che corrispondono al cambiare la scelta iniziale.

• (EN) Bapeswara Rao, V. V. e Rao, M. Bhaskara (1992). A three-door game show and some of its variants. The Mathematical Scientist 17(2), 89–94
• (EN) Bohl, Alan H.; Liberatore, Matthew J.; e Nydick, Robert L. (1995). A Tale of Two Goats... and a Car, or The Importance of Assumptions in Problem Solutions. Journal of Recreational Mathematics 1995, 1–9.
• Joseph Bertrand (1889). Calcul des probabilités
• (EN) Gardner, Martin (1959). Rubrica "Mathematical Games", Scientific American, ottobre 1959, 180–182.
• (EN) Mueser, Peter R. e Granberg, Donald (1999). The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making (University of Missouri Working Paper 99-06). http://econwpa.wustl.edu:80/eps/exp/papers/9906/9906001.html Archiviato il 10 dicembre 2004 in Internet Archive. (ultimo accesso: 5 luglio 2005).
• (EN) Nahin, Paul J. (2000). Duelling idiots and other probability puzzlers. Princeton University Press, Princeton, NJ, 192-193. ISBN 0-691-00979-1
• (EN) Selvin, Steve (1975a). A problem in probability (letter to the editor). American Statistician 29(1): 67 (febbraio 1975).
• (EN) Selvin, Steve (1975b). On the Monty Hall problem (letter to the editor). American Statistician 29(3): 134 (agosto 1975).
• (EN) Tierney, John (1991). Behind Monty Hall's Doors: Puzzle, Debate and Answer?, The New York Times 21 luglio 1991, Domenica, Section 1; Part 1; Page 1; Column 5
• vos Savant, Marilyn (1990). Rubrica Ask Marilyn, Parade Magazine 12 (17 febbraio 1990). [citata in Bohl et al., 1995]
• (EN) Adams, Cecil (1990). On 'Let's Make a Deal,' you pick Door #1. Monty opens Door #2--no prize. Do you stay with Door #1 or switch to #3?, The Straight Dope 2 novembre 1990. http://www.straightdope.com/classics/a3_189.html (consultata il 25 luglio 2005).
• (EN) Tijms, Henk (2004). Understanding Probability, Chance Rules in Everyday Life. Cambridge University Press, New York, 213-215.
• Haddon, Mark (2003). Lo strano caso del cane ucciso a mezzanotte Einaudi.
• Rosenthal, Jeffrey S. (2006). Le regole del caso, istruzioni per l'uso, Longanesi, Milano, ISBN 88-304-2370-X
• (EN) Rosenhouse, Jason (2009). The Monty Hall Problem, Oxford University Press ISBN 978-0-19-536789-8

• Paradosso delle tre carte

• Wikimedia Commons contiene immagini o altri file sul problema di Monty Hall

• Simulazione fino a 100.000 tentativi, su utenti.quipo.it.
• Simulatore giocabile del paradosso, su math.ucsd.edu.