La proiezione ortogonale di un cubo su un piano verticale. In algebra lineare e analisi funzionale , una proiezione è una trasformazione lineare
P
{\displaystyle P}
spazio vettoriale in sé stesso (endomorfismo ) che è idempotente , cioè tale per cui
P
2
=
P
{\displaystyle P^{2}=P}
immagine rimane inalterata).
Nonostante la definizione sia piuttosto astratta, si tratta di un concetto matematico simile (e in qualche modo legato) alla proiezione cartografica .
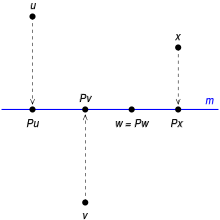
Proiezioni ortogonali
La trasformazione P è una proiezione ortogonale sulla retta m .
Nel piano cartesiano o nello spazio
In uno spazio euclideo , come ad esempio il piano cartesiano o lo spazio tridimensionale, una proiezione ortogonale su un determinato sottospazio
m
{\displaystyle m}
retta o un piano ) è una funzione
P
{\displaystyle P}
m
{\displaystyle m}
perpendicolare ad
m
{\displaystyle m}
Ad esempio, la proiezione del piano cartesiano sull'asse delle ascisse è la funzione:
(
x
,
y
)
↦
(
x
,
0
)
{\displaystyle (x,y)\mapsto (x,0)}
e la proiezione sulle ordinate è la funzione
(
x
,
y
)
↦
(
0
,
y
)
.
{\displaystyle (x,y)\mapsto (0,y).}
In uno spazio vettoriale
Se
S
{\displaystyle S}
sottospazio vettoriale
k
{\displaystyle k}
spazio euclideo
R
n
{\displaystyle \mathbb {R} ^{n}}
S
{\displaystyle S}
B
=
(
v
1
,
…
,
v
k
,
v
k
+
1
,
…
,
v
n
)
{\displaystyle B=(\mathbf {v} _{1},\ldots ,\mathbf {v} _{k},\mathbf {v} _{k+1},\ldots ,\mathbf {v} _{n})}
una base ortonormale per lo spazio euclideo, i cui primi
k
{\displaystyle k}
S
{\displaystyle S}
coordinate rispetto alla base
B
{\displaystyle B}
S
{\displaystyle S}
(
x
1
,
…
,
x
k
,
x
k
+
1
,
…
,
x
n
)
↦
(
x
1
,
…
,
x
k
,
0
,
…
,
0
)
.
{\displaystyle (\mathbf {x} _{1},\ldots ,\mathbf {x} _{k},\mathbf {x} _{k+1},\ldots ,\mathbf {x} _{n})\mapsto (\mathbf {x} _{1},\ldots ,\mathbf {x} _{k},0,\ldots ,0).}
In modo equivalente, se
v
{\displaystyle \mathbf {v} }
w
{\displaystyle \mathbf {w} }
R
n
{\displaystyle \mathbb {R} ^{n}}
⟨
⋅
,
⋅
⟩
{\displaystyle \langle \cdot ,\cdot \rangle }
prodotto scalare standard, si definisce proiezione di
v
{\displaystyle \mathbf {v} }
w
{\displaystyle \mathbf {w} }
c
w
{\displaystyle c\mathbf {w} }
c
=
⟨
v
,
w
⟩
⟨
w
,
w
⟩
{\displaystyle c={\langle \mathbf {v} ,\mathbf {w} \rangle \over \langle \mathbf {w} ,\mathbf {w} \rangle }}
è detto coefficiente di Fourier . I vettori
v
−
c
w
{\displaystyle \mathbf {v} -c\mathbf {w} }
w
{\displaystyle \mathbf {w} }
[ 1]
Operatore e matrice di proiezione
Un endomorfismo
f
:
V
→
V
{\displaystyle f\colon V\to V}
V
{\displaystyle V}
operatore di proiezione se è idempotente , cioè se
f
∘
f
=
f
{\displaystyle f\circ f=f}
Analogamente, una matrice quadrata
P
{\displaystyle P}
P
2
=
P
{\displaystyle P^{2}=P}
prodotto fra matrici ). Ad esempio:
P
=
[
1
0
0
0
1
0
0
0
0
]
{\displaystyle P={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}}
è una matrice di proiezione.
Questa nozione è strettamente collegata a quella di operatore di proiezione, poiché ogni matrice
n
×
n
{\displaystyle n\times n}
rappresenta un endomorfismo di
R
n
{\displaystyle \mathbb {R} ^{n}}
P
{\displaystyle P}
z
=
0
{\displaystyle z=0}
P
(
x
y
z
)
=
(
x
y
0
)
{\displaystyle P{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}x\\y\\0\end{pmatrix}}}
Le matrici seguenti rappresentano proiezioni ortogonali del piano
R
2
{\displaystyle \mathbb {R} ^{2}}
[
1
0
0
0
]
[
0
0
0
1
]
[
cos
2
θ
sin
θ
cos
θ
sin
θ
cos
θ
sin
2
θ
]
.
{\displaystyle {\begin{bmatrix}1&0\\0&0\end{bmatrix}}\qquad {\begin{bmatrix}0&0\\0&1\end{bmatrix}}\qquad {\begin{bmatrix}\cos ^{2}\theta &\sin \theta \cos \theta \\\sin \theta \cos \theta &\sin ^{2}\theta \\\end{bmatrix}}.}
La matrice seguente rappresenta una proiezione non ortogonale sulla retta delle ascisse:
[
1
1
0
0
]
.
{\displaystyle {\begin{bmatrix}1&1\\0&0\end{bmatrix}}.}
Se
P
,
P
1
,
P
2
{\displaystyle P,P_{1},P_{2}}
P
n
=
P
{\displaystyle P^{n}=P}
n
>
0
{\displaystyle n>0}
Gli autovalori possibili di
P
{\displaystyle P}
Se
P
1
{\displaystyle P_{1}}
P
2
{\displaystyle P_{2}}
P
1
P
2
=
P
2
P
1
=
0
{\displaystyle P_{1}P_{2}=P_{2}P_{1}=0}
P
=
P
1
+
P
2
{\displaystyle P=P_{1}+P_{2}}
Il nucleo e l'immagine di una proiezione sono in somma diretta.
Note
Bibliografia
Serge Lang, Algebra lineare , Torino, Bollati Boringhieri, 1992, ISBN 88-339-5035-2 . (EN Linear Operators, Part I: General Theory , Interscience, 1958. (EN Matrix Analysis and Applied Linear Algebra ISBN 978-0-89871-454-8 .
Voci correlate
Altri progetti
Collegamenti esterni