|
Grafentheorie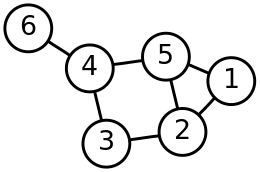
De grafentheorie is een deelgebied van de wiskunde dat de eigenschappen van grafen bestudeert. Een graaf bestaat uit een verzameling punten, knopen genoemd, waarvan sommige verbonden zijn door lijnen, de zijden, kanten, takken of bogen. Afhankelijk van de toepassing kunnen de lijnen gericht zijn, dan worden ze ook wel pijlen genoemd, men spreekt dan van een gerichte graaf. Ook worden wel gewichten aan de lijnen toegekend door middel van getallen, deze stellen dan bijvoorbeeld de afstand tussen twee punten voor. Een graaf met gewichten noemt men een gewogen graaf. Structuren die als grafen weergegeven kunnen worden, komen veel voor. Grafen worden bijvoorbeeld gebruikt om eindigetoestandsautomaten te modelleren, om een schematische routekaart te maken tussen een aantal plaatsen met de afstanden daartussen en bij patroonvergelijking. Verschillende soorten grafen spelen in de informatica nog een rol, niet alleen in de vorm van boomstructuren, maar ook om gegevensoverdracht over netwerken weer te geven. Er kunnen algoritmes worden uitgevoerd om bepaalde eigenschappen van zo'n graaf te berekenen en aan de hand daarvan voorspellingen te doen of beslissingen te nemen over de optimale route voor een datapakket. Dit is binnen de informatica dan ook een belangrijk onderwerp. Complexe netwerken vormen een vrij recent gebied in het onderzoek rond grafen, dat minder is gericht op de studie van kleine grafen en de eigenschappen van individuele knopen en zijden in deze grafen, maar eerder op de statistische eigenschappen van grootschalige netwerken. DefinitieEr zijn verschillende definities gangbaar om grafen te definiëren. Hier volgen de definities zoals ze in deze encyclopedie worden gehanteerd. Een graaf bestaat uit een verzameling knopen, punten of toppen, Engels: vertices, en een verzameling zijden, kanten, bogen of takken, Engels: edges, van paren knopen. Formeler: Een graaf is een geordend paar, waarin een willekeurige verzameling is en waarin een multiset bestaande uit multisets van twee al dan niet verschillende elementen uit . De elementen van heten de knopen van de graaf en de elementen van heten de zijden van . De knopen die een zijde vormen, heten de eindpunten van de zijde. Ter verduidelijking schrijft men ook
Een zijde verbindt twee verschillende knopen met elkaar of is een lus die bij dezelfde knoop terugkomt. Twee knopen kunnen door meer dan een zijde zijn verbonden. In de grafische voorstelling wordt soms, in plaats van elke zijde afzonderlijk, het aantal zijden tussen twee knopen weergegeven als één zijde met daarnaast een getal dat het aantal zijden voorstelt. Terminologie en notatieTerminologie en notatie voor alle hier besproken grafen:
Enkelvoudige graaf De enkelvoudige graaf is de meest gebruikte soort graaf. In een enkelvoudige graaf komen geen lussen voor en is er niet meer dan één zijde tussen twee knopen. De enkelvoudige graaf vindt veel toepassing binnen de wiskunde en de informatica. Over deze grafen is een groot aantal stellingen bewezen. Componenten en samenhangende grafen Binnen een enkelvoudige ongerichte graaf is een component van een deelgraaf waarbij tussen elk tweetal knopen van een wandeling is, en er geen wandeling is naar enige andere knoop. Dat betekent dat de zijden van een enkelvoudige ongerichte graaf alleen tussen de knopen in dezelfde component lopen. Een graaf die uit maar een component bestaat, dus waarin een wandeling tussen elk paar punten bestaat, is daarmee een samenhangende graaf. De componenten van een enkelvoudige ongerichte graaf zijn samenhangende deelgrafen. Een enkelvoudige ongerichte graaf valt in een partitie uiteen in onderling disjuncte componenten. Matrixvoorstelling van een graafEen eindige graaf kan eenvoudig voorgesteld worden in een matrix, de bogenmatrix. Zijde en boog zijn ten aanzien van grafen synoniem. De bogenmatrix is een vierkante matrix met dimensies , waarin het aantal knopen in de graaf is. Het element op rij en kolom in de bogenmatrix is 1 als er een zijde (boog) bestaat die van naar gaat en 0 als dit niet het geval is. Soms worden lussen dubbel geteld, zodat de graad van een knoop uit de bogenmatrix kan worden uitgelezen door de elementen in de overeenkomstige rij of kolom bij elkaar op te tellen. Hieronder doen we dat echter niet. Is de bogenmatrix opgesteld, dan kan deze worden gebruikt om af te lezen hoeveel wandelingen er van een knoop naar een andere zijn. Door de bogenmatrix tot de macht te verheffen, kan men in de kolom op rij aflezen hoeveel wandelingen er zijn van lengte van knoop naar knoop . In het bovenstaande voorbeeld is Er zijn dus bijvoorbeeld drie wandelingen van lengte drie van knoop 4 naar knoop 6, namelijk 4~3~4~6, 4~5~4~6, en 4~6~4~6. Voor een enkelvoudige graaf zonder lussen kan een matrix worden gemaakt, waarin op de hoofddiagonaal de graad van ieder van de knopen in de graaf staan. Er geldt dan dat in de matrix van Laplace de som van de elementen in alle rijen en in alle kolommen gelijk is aan 0. De graad van knoop 1 is drie en dat is ook de som van de elementen in zowel de eerste rij als in de eerste kolom van de bogenmatrix. Komen er in een graaf veel meer knopen dan zijden voor, dan is het gunstig om de graaf in een incidentiematrix vast te leggen. Is het aantal zijden in de graaf, dan is de incidentiematrix een -matrix. BoomEen boomstructuur is een samenhangende graaf zonder cykels. Een samenhangende graaf zonder cykels heet een boom, omdat een dergelijke graaf in een tekening vaak op een boom lijkt. Een boom heeft één zijde minder dan het aantal knopen. Een boom met de verzameling knopen heeft dus zijden.
Bewijs
Het bewijs gaat met volledige inductie naar het aantal knopen.
 Het is bij algoritmes op bomen vaak handig en ook gebruikelijk om een knoop in de boom aan te wijzen en deze een speciale status binnen de boom te geven, vaak wordt deze knoop gezien als het 'begin' van de boom. Deze knoop wordt dan de wortel van de boom genoemd. Bomen behoren tot de fundamentele structuren in de wiskunde en de informatica. Bomen worden vaak gebruikt om model te staan voor verzamelingen van objecten met een bepaalde hiërarchie en zijn terug te vinden in bijvoorbeeld:
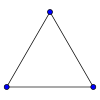
De veelvuldigheid en populariteit van bomen maakt dat er voor bomen als zodanig vele algoritmen gedefinieerd zijn. Voorbeelden hiervan zijn Cykelgraaf De cykelgraaf met knopen is de enkelvoudige, samenhangende graaf met knopen, waarin iedere knoop verbonden is met twee andere. Een dergelijke graaf heeft de vorm van een cirkel en er komen evenveel knopen als zijden in voor. De cykelgraaf met het minste aantal knopen en zijden is de volledige graaf . Cykelgrafen zijn binnen de informatica zeer bekend als netwerkmodel. Het Token Ring netwerk is hierop gebaseerd. Cykelgrafen dienen ook vaak als model voor lokale zoekalgoritmen. Volledige graafDe volledige graaf met knopen is de graaf waarin elke knoop met elke andere knoop verbonden is. De volgende grafen zijn voorbeelden van volledige grafen:
Het aantal zijden van is , het -ste driehoeksgetal.
Bewijs
Het aantal zijden is gelijk aan het aantal mogelijke paren knopen, dus het aantal manieren om uit objecten er twee te kiezen. Dat aantal is de binomiaalcoëfficiënt .
Een clique of kliek is een deelverzameling knopen waarin elke knoop verbonden is met alle andere knopen in die deelverzameling. Samen met de zijden waarmee ze verbonden zijn, vormen ze een volledige graaf. Euler en HamiltonDe wiskundige Leonhard Euler heeft zich onder meer beziggehouden met het probleem van de zeven bruggen van Koningsbergen. Dit probleem komt neer op de vraag of het mogelijk is in een samenhangende graaf, zoals bij de zeven bruggen, een wandeling te vinden waarin alle zijden één keer voorkomen. Zo'n wandeling heet een eulerwandeling. Het is ook de vraag dat een dergelijke wandeling bestaat zodat deze begint en eindigt in dezelfde knoop, dat heet een eulercykel. Een eulergraaf is een graaf met een eulercykel. Euler heeft dit probleem in 1736 opgelost. Wat betreft het tweede probleem bewees hij het volgende: Een samenhangende graaf bevat dan en slechts dan een eulercykel als de graad van alle knopen even is.
Bewijs
De grafen en bevatten beide eulercykels. De graaf die het probleem van de zeven bruggen voorstelt, bevat geen eulercykel. De voorwaarde voor een eulerwandeling is iets minder streng. Een samenhangende graaf bevat een eulerwandeling dan en slechts dan als de graad van alle knopen, eventueel op twee na, even is.
Bewijs
Behalve de eulercykels en -wandelingen is er nog een variant: de cykel en de wandeling, waarin iedere knoop één keer voorkomt. Dit zijn de hamiltoncykel en hamiltonwandeling. Deze variant is bedacht door William Hamilton. Er bestaat geen karakteristiek van grafen die een hamiltoncykel bevatten. De wiskundige Øystein Ore bewees wel de volgende stelling: De graaf bevat een hamiltoncykel als de som van de graden van elk tweetal niet-verbonden knopen samen groter is dan het aantal knopen van de graaf. Over het algemeen is het vinden van een hamiltoncykel in een graaf een NP-volledig probleem; dit in tegenstelling tot het zoeken naar een eulercykel dat in polynomiale tijd kan worden opgelost dankzij de bovengenoemde regels. Een hamiltoncykel is een eenvoudig geval van het handelsreizigersprobleem. Bij dit probleem worden ook afstanden aan de verbindingen tussen de knopen of plaatsen toegevoegd en is het de opdracht de kortste rondreis te bepalen. Overige grafenBipartiete graaf Een bipartiete graaf is een graaf waarvan de knopen verdeeld zijn over een partitie met de eigenschap dat een knoop in de ene partitie alleen verbonden is met knopen in de andere partitie.
Hierbij is het ook toegestaan dat een van beide partities leeg is, of zelfs allebei, zodat ook een graaf op 0 of 1 knoop bipartiet is. De volledige bipartiete graaf met knopen in en knopen in , waarin alle knopen in met alle knopen in verbonden zijn, wordt genoteerd als . Eveneens is duidelijk dat de kleinste, niet-bipartiete graaf is. Met dit inzicht valt ook goed in te zien dat een graaf niet-bipartiet is, als deze een cykel van oneven lengte bevat. Met name geldt voor alle grafen dat deze niet bipartiet zijn, sterker nog: Een graaf is bipartiet bevat geen oneven cykels
Bewijs
Er zijn ook -partiete grafen, waarbij de graaf wordt opgesplitst in partities waarvoor er wederom geen lijnen zijn tussen punten in dezelfde partitie. Voor heb je weer de bipartiete graaf. Planaire graafPlanaire of vlakke grafen zijn grafen die op een plat vlak kunnen worden getekend zonder dat de zijden van de graaf elkaar snijden. Dergelijke grafen zijn van belang bij de modellering van zaken als pijpleidingen en printplaten voor elektronica, waar de verbindingen geen contact mogen maken. Wat dat eerste betreft zijn planaire grafen dan ook bij het grotere publiek bekend in de vorm van puzzeltjes zoals "probeer drie huizen aan te sluiten op de gas-, water- en elektra-bronnen, zonder dat enige van de leidingen elkaar snijden". Dit is in feite de vraag of planair is. Ook over planaire grafen heeft Leonhard Euler nagedacht en hij vond de stelling van Euler. Deze stelling is gebaseerd op het aantal knopen, zijden en gebieden van een graaf. Een gebied van een graaf is een deel van de graaf dat geheel door zijden of door buitenste knopen van de graaf wordt omgeven. Men kan een gebied zien als een gedeelte van het papier waarop de graaf is getekend. Het aantal gebieden hangt ervan af hoe de graaf precies getekend wordt, maar het blijkt dat een bepaalde graaf altijd met een aantal gebieden kan worden getekend dat niet verandert, hoe de graaf ook precies is getekend, behalve als de graaf niet-planair is getekend.
Zij een samenhangende, planaire graaf met knopen, zijden en gebieden. Dan geldt
Bewijs
Het bewijs gaat met inductie naar . Omdat samenhangend is, geldt altijd . Stel , de graaf is dan een boom. Aangezien geen cykels bevat, is het aantal gebieden 1. Dus Inductiestap: Neem aan dat voor alle vlakke grafen met geldt dat . We moeten bewijzen dat voor een willekeurige vlakke graaf met de eigenschap ook geldt. De graaf bevat nu een cykel. Deze cykel scheidt een apart gebied af. Verwijderen we nu een zijde uit de cykel, dan hebben we een graaf met een zijde en een gebied minder. Als we het aantal knopen, zijden en gebieden in deze graaf en noemen, geldt
dus vanwege de inductiehypothese: Hieruit kunnen we afleiden dat
Met de stelling van Euler kan aangetoond worden dat een samenhangende graaf alleen planair kan zijn als hij niet al te veel zijden heeft. Zij een samenhangende, planaire graaf met knopen en zijden. Dan geldt
Bewijs
Het idee achter de stelling is dat er een relatie is tussen het aantal zijden in en het soort gebieden waarin het vlak verdeelt. Iedere zijde fungeert in een planaire muur als "binnenmuur" en als "buitenmuur" van een (afgesloten) gebied – de "buitenkant" van de graaf telt als één groot gebied. Tellen we alle binnen- en buitenmuren, dan komen we aan (iedere zijde tel je zo twee keer). Verder is het zo dat ieder gebied afgezonderd door de graaf een bepaalde vorm heeft: driehoek, vierhoek, vijfhoek, etc. Iedere -hoek heeft dan binnenmuren. Noemen we het aantal driehoekige gebieden , het aantal vierhoekige , het aantal vijfhoekige , enz., dan kunnen we het aantal muren ook op een andere manier tellen:
zodat Dus we weten ook dat Dat betekent waaruit volgt: Met deze informatie in de hand, kunnen we zo narekenen dat bijvoorbeeld niet planair is. Op een soortgelijke manier als hierboven, kunnen we ook bewijzen voor samenhangende planaire grafen zonder driehoeken, dus met het "kleinste" gebied een vierhoek, dat . Hiermee is ook het puzzeltje opgelost: is niet planair. Volgens de stelling van Kuratowski is een graaf planair dan en slechts dan als er in geen subgrafen voorkomen die isomorf zijn met een subdivisie van of . Kazimierz Kuratowski heeft de stelling in 1930 bewezen. De wiskundige Karl Menger heeft ook in 1930 een soortgelijke stelling bewezen voor grafen waarin alle knopen de orde drie hebben. Het is in dat geval een nodige en voldoende voorwaarde dat er in geen subgraaf voorkomt die isomorf is met een subdivisie van . Petersengraaf De volgende graaf staat bekend als de Petersengraaf, gedefinieerd door de Deense wiskundige Petersen. Op zich is er niets speciaals mee aan de hand; de Petersengraaf komt echter binnen de grafentheorie vaak voor, als voorbeeld bij bewijzen of als tegenvoorbeeld om stellingen mee te ontkrachten. De Petersengraaf wordt dan vaak gebruikt als deelgraaf van een andere, meer complexe graaf. De Petersengraaf bevat een subdivisie van . Hij heeft ook als minor: als we de buitenste "ring" van knopen en de binnenste "ring" samentrekken, vinden we de -graaf. We kunnen dan ook duidelijk zien dat de Petersengraaf niet planair is. Graafoperaties, de 2-graaf en geïnduceerde grafen Uitgaande van een graaf (of een aantal verschillende grafen) kunnen we, via allerlei operaties, andere grafen maken. Om te beginnen is er de op geïnduceerde graaf Deze graaf is gedefinieerd door: met en zo dat voor alle knopen geldt De door geïnduceerde graaf is de graaf bestaande uit een aantal knopen van en de bijbehorende zijden van .  Daarnaast is er de complementgraaf of complementaire graaf van gedefinieerd door: met en zo dat voor alle knopen geldt De complementgraaf van heeft dus dezelfde knopen als , maar alle mogelijke zijden die juist niet in zitten.  Ook is er de lijngraaf van , die de zijden van als knopen heeft. De knopen van worden verbonden door een zijde, als de oorspronkelijke zijden van - bij knopen - een knoop gemeen hebben. Deze graaf is gedefinieerd door:
 Voor twee grafen die geen knopen of zijden gemeen hebben, kan ook de vereniging en het cartesisch product gedefinieerd worden. De vereniging van en is de graaf met  Het cartesisch product van en is de graaf met als knopen de paren van knopen van en en twee dergelijke knopen zijn verbonden door een zijde als een van de knopen in de twee paren dezelfde zijn en de andere verbonden waren. De vereniging is dus gedefinieerd door:
 Een bekend voorbeeld van graaf-vermenigvuldiging is de rij van de 'machten' van de 2-graaf : dit zijn de -dimensionale kubussen hier rechts. Gerichte grafen Een type graaf die naast de enkelvoudige graaf vaak voorkomt, is de gerichte graaf. Formeel is een gerichte graaf een graaf met Het verschil met de enkelvoudige graaf is dat de zijden niet langer ongeordende paren zijn, maar juist geordende paren (intuïtief wil dat zeggen: de zijden hebben een richting). Merk op dat in de bovenstaande definitie een zijde een geordend paar is en niet een verzameling. Dit betekent dat de zijde niet dezelfde is als de zijde . Vanwege de richting is het normaal om bij een gerichte graaf de zijden als pijlen te tekenen. Veel van de concepten zoals die gedefinieerd zijn voor enkelvoudige grafen, bestaan ook voor gerichte grafen. Bomen, volledige grafen, somgrafen en productgrafen bestaan allemaal. Alleen is de uitwerking soms anders, omdat de richting nu meespeelt. Zo is het bij enkelvoudige grafen zo dat er voor iedere knoop zijde maar één pad is van de wortel naar ; bij een gerichte graaf kunnen er meerdere zijn, zonder dat dit een cykel oplevert. Gerichte grafen worden vaak toegepast in de modellering van problemen waarbij het niet zinnig is om paden in meer dan één richting te doorlopen. Gebruik je bijvoorbeeld een graaf om aan tijdsplanning te doen voor de bouw van een woning, dan heeft het alleen zin om de bouw van de fundering voor de bouw van de muren plaats te laten vinden en andersom heeft geen zin. Enige verschillen ten opzichte van enkelvoudige grafenEr zijn een aantal typische dingen die anders zijn in gerichte grafen in vergelijking met enkelvoudige grafen. Graad heeft bijvoorbeeld een andere betekenis. De graad van een knoop is in een enkelvoudige graaf het aantal zijden waarmee de knoop verbonden is; in een gerichte graaf is de definitie iets anders:
Een gerichte graaf bevat dan en slechts dan een eulerwandeling als voor alle knopen in de graaf de in- en uitgraad aan elkaar gelijk zijn. Het bewijs hiervoor is vrijwel hetzelfde als dat voor de enkelvoudige eulergraaf. Een gerichte graaf heet samenhangend als er voor iedere partitie een zijde loopt van naar of omgekeerd. Loopt er altijd een dergelijke zijde in beide richtingen, dat wil zeggen als er tussen iedere twee knopen een wandeling is in beide richtingen, dan heet de graaf sterk samenhangend. Gelabelde en gewogen grafenEen andere uitbreiding op de enkelvoudige graaf die vaak voorkomt is die van labeling. Hierbij wordt de graaf uitgebreid met een of twee functies en De functies voegt aan iedere zijde, en de functie aan iedere knoop een element toe uit een of andere verzameling symbolen. Het labelen van de zijden komt meer voor dan labelen van de knopen. Als de symbolen getallen zijn (, etc.), noemen we de labeling een weging. De graaf heet dan een gewogen graaf. Een gewogen, gerichte graaf wordt ook wel een netwerk genoemd. Labeling en met name weging worden gebruikt om aan een graaf speciale betekenissen toe te kennen. Wordt een graaf gebruikt als model voor een wegennet bij routeplanning, dan kan bij een weging bijvoorbeeld gedacht worden aan de lengte van de weg, of de drukte. Optimaliseringsproblemen op grafen gebruiken meestal weging als criterium aan de hand waarvan wordt geoptimaliseerd. Het aantal gelabelde bomen op knopen is
Bewijs
Het bewijs volgt uit de codering van Prüfer van knoop-gelabelde bomen. Deze constructie werkt als volgt:
HypergrafenHypergrafen zijn een veralgemening van grafen, in zoverre dat in een hypergraaf een hyperzijde een willekeurig aantal knopen kan verbinden, gaande van 1 tot het aantal knopen in de graaf. Problemen op grafen
Belangrijke algoritmes op grafen
Gerelateerde wiskundige gebiedenWebsites
Zie de categorie Graph theory van Wikimedia Commons voor mediabestanden over dit onderwerp.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||