Krožnica (krog ) z obsegom
C
{\displaystyle C\!\,}
premerom
D
{\displaystyle D\!\,}
R
{\displaystyle R\!\,}
središčem
O
{\displaystyle O\!\,}
Polmér (tudi pôlmér in pólmér [ 1] rádij [ 2] [ 3] krožnice (kroga ) ali sfere (krogle je v klasični geometriji poljubna daljica od središča do oboda kroga ali površine sfere, v modernejši rabi pa tudi dolžina daljice (razdalja ). V znanosti in tehniki se izraz polmer ukrivljenosti pogosto rabi kot sopomenka za polmer.
Polmer ima lahko za različne geometrijske figure tudi več specifičnih definicij, kot na primer za elipso .
Ime radij je tujka , prevzeta prek nemške besede Radius , ta pa izhaja iz latinske besede radius , kar pomeni polmer , (sončni) žarek napero (špico ) kolesa voza merilna palica [ 4] [ 5] Petrusu Ramusu , nekoliko kasneje pri Françoisu Viètu , splošno sprejet pa je postal šele konec 17. stoletja.
Tipična okrajšava in ime matematične spremenljivke za polmer je
r
{\displaystyle r\!\,}
R
{\displaystyle R\!\,}
premer
d
{\displaystyle d\!\,}
D
{\displaystyle D\!\,}
[ 6]
d
≐
2
r
⇒
r
=
d
2
.
{\displaystyle d\doteq 2r\quad \Rightarrow \quad r={\frac {d}{2}}\!\,.}
Če objekt nima središča, se izraz lahko nanaša na polmer njegove očrtane krožnice ali očrtane sfere . V obeh primerih je lahko polmer večji od polovice premera, ki je običajno opredeljen kot največja razdalja med poljubnima točkama figure. Polmer včrtane krožnice geometrijske figure je običajno polmer največje krožnice kroga ali sfere, ki jo vsebuje. Notranji polmer obroča , cevi ali drugega votlega objekta je polmer njegove votline.
Za pravilne mnogokotnike je polmer enak polmeru njegove očrtane krožnice.[ 7] apotema .
V teoriji grafov je polmer grafa minimum vseh točk
u
{\displaystyle u\!\,}
razdalje od
u
{\displaystyle u\!\,}
grafa .[ 8]
Pri mnogih geometrijskih figurah ima polmer dobro definirano razmerje z drugimi merami figure.
Polmer krožnice (kroga) z obsegom
o
{\displaystyle o\!\,}
r
=
o
2
π
.
{\displaystyle r={\frac {o}{2\pi }}\!\,.}
Polmer kroga s ploščino
p
{\displaystyle p\!\,}
r
=
p
π
.
{\displaystyle r={\sqrt {\frac {p}{\pi }}}\!\,.}
Polmer krožnice, ki poteka skozi tri nekolinearne točke
P
1
{\displaystyle P_{1}\!\,}
P
2
{\displaystyle P_{2}\!\,}
P
3
{\displaystyle P_{3}\!\,}
r
=
|
O
P
1
→
−
O
P
3
→
|
2
sin
θ
,
{\displaystyle r={\frac {|{\vec {OP_{1}}}-{\vec {OP_{3}}}|}{2\sin \theta }}\!\,,}
kjer je
θ
{\displaystyle \theta \!\,}
kot
∠
P
1
P
2
P
3
{\displaystyle \angle P_{1}P_{2}P_{3}\!\,}
sinusni izrek . Če so tri točke podane s svojimi koordinatami
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})\!\,}
(
x
2
,
y
2
)
{\displaystyle (x_{2},y_{2})\!\,}
(
x
3
,
y
3
)
{\displaystyle (x_{3},y_{3})\!\,}
r
=
(
(
x
2
−
x
1
)
2
+
(
y
2
−
y
1
)
2
)
(
(
x
2
−
x
3
)
2
+
(
y
2
−
y
3
)
2
)
(
(
x
3
−
x
1
)
2
+
(
y
3
−
y
1
)
2
)
2
|
x
1
y
2
+
x
2
y
3
+
x
3
y
1
−
x
1
y
3
−
x
2
y
1
−
x
3
y
2
|
.
{\displaystyle r={\frac {\sqrt {{\bigl (}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}{\bigr )}{\bigl (}(x_{2}-x_{3})^{2}+(y_{2}-y_{3})^{2}{\bigr )}{\bigl (}(x_{3}-x_{1})^{2}+(y_{3}-y_{1})^{2}{\bigr )}}}{2{\bigl |}x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{2}y_{1}-x_{3}y_{2}{\bigr |}}}\!\,.}
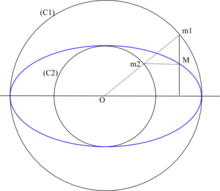
Elipsa
Elipsi očrtana in včrtana krožnica Za elipso se lahko opredeli več pojmov polmera, pojmov, ki vračajo klasični polmer v primeru krožnice.
r
1
=
a
+
b
2
.
{\displaystyle r_{1}={\frac {a+b}{2}}\!\,.}
površinski polmer je polmer kroga s površino, enako površini elipse. Enak je kvadratnemu korenu produkta obeh polosi elipse:
r
2
=
a
b
=
a
1
−
e
2
4
,
{\displaystyle r_{2}={\sqrt {ab}}=a{\sqrt[{4}]{1-e^{2}}}\!\,,}
kjer je
e
{\displaystyle e\!\,}
izsrednost elipse. To je torej geometrična sredina obeh njenih polosi. še en izjemen polmer elipse je povprečna razdalja od točke, ki se giblje po elipsi s konstantno hitrostjo , do gorišča te elipse. Ta polmer, ki je po definiciji enak:
r
3
=
∫
0
2
π
(
a
(
cos
E
−
e
)
2
+
b
2
sin
2
E
a
2
sin
2
E
+
b
2
cos
2
E
d
E
∫
0
2
π
a
2
sin
2
E
+
b
2
cos
2
E
d
E
,
{\displaystyle r_{3}={\frac {\int _{0}^{2\pi }{\sqrt {(a(\cos E-e)^{2}+b^{2}\sin ^{2}E}}\,{\sqrt {a^{2}\sin ^{2}E+b^{2}\cos ^{2}E}}\operatorname {d} \!E}{\int _{0}^{2\pi }{\sqrt {a^{2}\sin ^{2}E+b^{2}\cos ^{2}E}}\operatorname {d} \!E}}\!\,,}
se poenostavi na vrednost velike polosi
r
3
=
a
{\displaystyle r_{3}=a\!\,}
povprečna razdalja od točke, ki se giblje po elipsi s konstantno hitrostjo, do središča te elipse:
r
4
=
∫
0
2
π
a
2
cos
2
E
+
b
2
sin
2
E
a
2
sin
2
E
+
b
2
cos
2
E
d
E
∫
0
2
π
a
2
sin
2
E
+
b
2
cos
2
E
d
E
.
{\displaystyle r_{4}={\frac {\int _{0}^{2\pi }{{\sqrt {a^{2}\cos ^{2}E+b^{2}\sin ^{2}E}}\,{\sqrt {a^{2}\sin ^{2}E+b^{2}\cos ^{2}E}}\operatorname {d} \!E}}{\int _{0}^{2\pi }{{\sqrt {a^{2}\sin ^{2}E+b^{2}\cos ^{2}E}}\operatorname {d} \!E}}}\!\,.}
Izraz ne daje enostavne vrednosti. povprečna razdalja do središča elipse pri konstantni hitrosti ekscentrične anomalije
E
{\displaystyle E\!\,}
r
5
=
1
2
π
∫
0
2
π
a
2
cos
2
E
+
b
2
sin
2
E
d
E
{\displaystyle r_{5}={\frac {1}{2\pi }}{\int _{0}^{2\pi }{{\sqrt {a^{2}\cos ^{2}E+b^{2}\sin ^{2}E}}\operatorname {d} \!E}}\!\,}
je enaka
o
2
π
{\displaystyle {\frac {o}{2\pi }}\!\,}
o
{\displaystyle o\!\,}
∬
(
M
1
M
2
)
2
d
M
1
d
M
2
∬
d
M
1
d
M
2
,
{\displaystyle {\sqrt {\frac {\iint (M_{1}M_{2})^{2}\operatorname {d} \!M_{1}\operatorname {d} \!M_{2}}{\iint \operatorname {d} \!M_{1}\operatorname {d} \!M_{2}}}}\!\,,}
ali:
∫
0
1
∫
0
1
∫
0
2
π
∫
0
2
π
(
(
a
r
1
cos
E
1
−
b
r
2
cos
E
2
)
2
+
(
a
r
1
cos
E
1
−
b
r
2
cos
E
2
)
2
)
r
1
r
2
d
r
1
d
r
2
d
E
1
d
E
2
∫
0
1
∫
0
1
∫
0
2
π
∫
0
2
π
r
1
r
2
d
r
1
d
r
2
d
E
1
d
E
2
,
{\displaystyle {\sqrt {\frac {\int _{0}^{1}\int _{0}^{1}\int _{0}^{2\pi }\int _{0}^{2\pi }((ar_{1}\cos E_{1}-br_{2}\cos E_{2})^{2}+(ar_{1}\cos E_{1}-br_{2}\cos E_{2})^{2})r_{1}r_{2}\operatorname {d} \!r_{1}\operatorname {d} \!r_{2}\operatorname {d} \!E_{1}\operatorname {d} \!E_{2}}{\int _{0}^{1}\int _{0}^{1}\int _{0}^{2\pi }\int _{0}^{2\pi }r_{1}r_{2}\operatorname {d} \!r_{1}\operatorname {d} \!r_{2}\operatorname {d} \!E_{1}\operatorname {d} \!E_{2}}}}\!\,,}
kar se poenostavi na kvadratno sredino obeh polosi
r
6
=
a
2
+
b
2
2
{\displaystyle r_{6}={\sqrt {\frac {a^{2}+b^{2}}{2}}}\!\,}
Pravilni mnogokotniki
n
{\displaystyle n\!\,}
R
n
{\displaystyle R_{n}\!\,}
3
3
3
=
0
,
577
350
…
{\displaystyle {\frac {\sqrt {3}}{3}}=0,577\,350\ldots \!\,}
4
2
2
=
0
,
707
106
…
{\displaystyle {\frac {\sqrt {2}}{2}}=0,707\,106\ldots \!\,}
5
0
,
850
650
…
{\displaystyle 0,850\,650\ldots \!\,}
6
1
{\displaystyle 1\!\,}
7
1
,
152
382
…
{\displaystyle 1,152\,382\ldots \!\,}
8
1
,
306
562
…
{\displaystyle 1,306\,562\ldots \!\,}
9
1
,
461
902
…
{\displaystyle 1,461\,902\ldots \!\,}
10
1
,
618
033
…
{\displaystyle 1,618\,033\ldots \!\,}
11
1
,
774
732
…
{\displaystyle 1,774\,732\ldots \!\,}
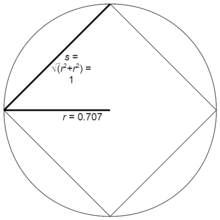
Zgled za kvadrat
(
n
=
4
)
{\displaystyle (n=4)\!\,}
Polmer
r
n
{\displaystyle r_{n}\!\,}
pravilnega mnogokotnika z
n
{\displaystyle n\!\,}
stranicami dolžine
s
n
{\displaystyle s_{n}\!\,}
r
n
=
R
n
s
n
{\displaystyle r_{n}=R_{n}s_{n}\!\,}
R
n
=
1
2
sin
π
n
.
{\displaystyle R_{n}={\frac {1}{2\sin \displaystyle {\frac {\pi }{n}}}}\!\,.}
Vrednosti
R
n
{\displaystyle R_{n}\!\,}
n
{\displaystyle n\!\,}
s
=
1
{\displaystyle s=1\!\,}
Z dolžinami apotem
r
a
,
n
{\displaystyle r_{{\rm {a}},n}\!\,}
r
n
=
r
a
,
n
cos
π
n
.
{\displaystyle r_{n}={\frac {r_{{\rm {a}},n}}{\cos \displaystyle {\frac {\pi }{n}}}}\!\,.}
Elipsoid
Za elipsoid s polosmi
a
⩾
b
⩾
c
{\displaystyle a\geqslant b\geqslant c\!\,}
Povprečni polmer elipsoida je enak aritmetični sredini vseh njegovih treh polosi:
r
1
=
a
+
b
+
c
3
.
{\displaystyle r_{1}={\frac {a+b+c}{3}}\!\,.}
Volumetrični polmer elipsoida je enak polmeru navidezne krogle s prostornino , enako prostornini obravnavanega elipsoida. Je enak geometrični sredini vseh njegovih treh polosi:
r
2
=
a
b
c
3
.
{\displaystyle r_{2}={\sqrt[{3}]{abc}}\!\,.}
Avtalni polmer
Avtalni polmer (enakopovršinski polmer) elipsoida je enak polmeru navidezne krogle s površino, enako površini obravnavanega elipsoida
P
{\displaystyle P\!\,}
r
3
=
P
π
.
{\displaystyle r_{3}={\sqrt {\frac {P}{\pi }}}\!\,.}
V primeru podolgovatega sferoida (vrtenje elipse okrog glavne osi ) je polmer na primer enak:
r
3
=
b
2
2
+
a
b
2
arcsin
e
e
.
{\displaystyle r_{3}={\sqrt {{\frac {b^{2}}{2}}+{\frac {ab}{2}}{\frac {\arcsin e}{e}}}}\!\,.}
Hiperkocke
Polmer
d
{\displaystyle d\!\,}
hiperkocke (
d
{\displaystyle d\!\,}
s
d
{\displaystyle s_{d}\!\,}
r
d
=
s
d
2
d
.
{\displaystyle r_{d}={\frac {s_{d}}{2}}{\sqrt {d}}\!\,.}
Raba v koordinatnih sistemih
Polarni koordinati
Polarni koordinatni sistem
(
r
,
ϕ
)
{\displaystyle (r,\phi )\!\,}
dvorazsežni koordinatni sistem , v katerem je vsaka točka na ravnini določena z razdaljo od fiksne točke in kotom od fiksne smeri.
Fiksna točka (analogna izhodišču kartezičnega koordinatnega sistema ) se imenuje pol polarna os radialna koordinata radij , kot pa kotna koordinata polarni kot azimut [ 9]
V cilindričnem koordinatnem sistemu
(
r
,
ϕ
,
z
)
{\displaystyle (r,\phi ,z)\!\,}
pravokotna na to os. Izhodišče sistema je točka, kjer so lahko vse tri koordinate podane kot nič. To je presečišče med referenčno ravnino in osjo.
Os se različno imenuje cilindrična ali vzdolžna os, da se jo loči od polarne osi – žarka , ki leži v referenčni ravnini in se začne pri izhodišču in kaže v referenčni smeri.
Razdalja od osi se imenuje radialna razdalja ali radij , medtem ko se kotna koordinata včasih imenuje kotna lega ali azimut . Radij in azimut se skupaj imenujeta polarni koordinati , saj ustrezata dvorazsežnemu polarnemu koordinatnemu sistemu v ravnini skozi točko, ki je vzporedna z referenčno ravnino. Tretja koordinata se imenuje višina altituda vodoravna ), vzdolžna lega [ 10] osna lega .[ 11]
Sferne koordinate
V sfernem koordinatnem sistemu
(
r
,
θ
,
ϕ
)
{\displaystyle (r,\theta ,\phi )\!\,}
r
{\displaystyle r\!\,}
lego opredeljuje polarni kot, izmerjen med radialno smerjo in fiksno smerjo zenita , in azimutni kot, kot med pravokotno projekcijo radialne smeri na referenčno ravnino, ki poteka skozi koordinatno izhodišče in je pravokotna na zenit in fiksno referenčno smer v tej ravnini.
Glej tudi
Sklici
↑ »polmér« , fran.si , Fran , Slovar slovenskega knjižnega jezika , pridobljeno 23. septembra 2024 ↑ »rádij« , fran.si , Fran, Slovar slovenskega knjižnega jezika, pridobljeno 23. septembra 2024 ↑ »radius« , merriam-webster.com (v angleščini), Merriam-Webster , pridobljeno 22. maja 2012 ↑ Snoj (2015) .↑ »radius« , dictionary.com (v angleščini), Dictionary.com , pridobljeno 8. avgusta 2009 ↑ »Radius of a Circle or Sphere« , mathwords.com (v angleščini), pridobljeno 8. avgusta 2009 ↑ Rich; Thomas (2008) .↑ Gross; Yellen (2006) .↑ Brown (1997) .↑ Krafft; Volokitin (2002) .↑ Groisman; Steinberg (1997) .
Viri
Brown, Richard G. (1997), Gleason, Andrew Mattei (ur.), Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis ISBN 0-395-77114-5 OCLC 36836350 ISBN 978-0-39-577114-3 Groisman, Alexander; Steinberg, Victor (24. februar 1997), »Solitary Vortex Pairs in Viscoelastic Couette Flow«, Physical Review Letters Ameriško fizikalno društvo (APS), 78 (8): 1460–1463, arXiv :patt-sol/9610008 Bibcode :1997PhRvL..78.1460G , doi :10.1103/physrevlett.78.1460 , ISSN 0031-9007 , S2CID 54814721 , [...]kjer so r , θ in z cilindrične koordinate [...] kot funkcija osne lege[...] Gross, Jonathan L.; Yellen, Jay (2006), Graph theory and its applications COBISS 27163909 , ISBN 1-58488-505-X OCLC 61458362 , pridobljeno 8. avgusta 2009 ISBN 978-1-58-488505-4 Krafft, Catherine; Volokitin, Alexander S. (1. junij 2002), »Resonant electron beam interaction with several lower hybrid waves« , Physics of Plasmas 9 (6): 2786–2797, Bibcode :2002PhPl....9.2786K , doi :10.1063/1.1465420 , ISSN 1089-7674 , arhivirano iz prvotnega spletišča dne 14. aprila 2013, pridobljeno 9. februarja 2013 , ...v cilindričnih koordinatah (r ,θ ,z ) ... in Z=vbz t je vzdolžna lega... Rich, Barnett; Thomas, Christopher (2008), Schaum's Outline of Geometry ISBN 0-07-154412-7 OCLC 299054572 , pridobljeno 8. avgusta 2009 ISBN 978-0-07-154412-2 Snoj, Marko (2015), »rādij« , fran.si , Fran, Slovenski etimološki slovar , pridobljeno 23. septembra 2024 Stöcker, Horst (2006), Matematični priročnik z osnovami računalništva , Ljubljana: Tehniška založba Slovenije , str. 53, 59, COBISS 229576192 , ISBN 86-365-0587-9 OCLC 449201276
Zunanje povezave

























![{\displaystyle r_{2}={\sqrt {ab}}=a{\sqrt[{4}]{1-e^{2}}}\!\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc652e4844dacaa73fcd005d083a0fc3e662aae)































![{\displaystyle r_{2}={\sqrt[{3}]{abc}}\!\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98266fb1cd76fb2d886b3833c24bc8d247380e6f)







