การแยกตัวประกอบ

บทความนี้ไม่มีการอ้างอิงจากแหล่งที่มาใด กรุณาช่วยปรับปรุงบทความนี้ โดยเพิ่มการอ้างอิงแหล่งที่มาที่น่าเชื่อถือ เนื้อความที่ไม่มีแหล่งที่มาอาจถูกคัดค้านหรือลบออก (เรียนรู้ว่าจะนำสารแม่แบบนี้ออกได้อย่างไรและเมื่อไร)

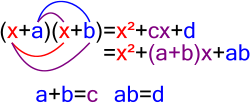การแยกตัวประกอบ (อังกฤษ: factorization) ในทางคณิตศาสตร์ หมายถึงการแบ่งย่อยวัตถุทางคณิตศาสตร์ (เช่น จำนวน พหุนาม หรือเมทริกซ์) ให้อยู่ในรูปผลคูณของวัตถุอื่น ซึ่งเมื่อคูณตัวประกอบเหล่านั้นเข้าด้วยกันจะได้ผลลัพธ์ดังเดิม ตัวอย่างเช่น จำนวน 15 สามารถแยกตัวประกอบให้เป็นจำนวนเฉพาะได้เป็น 3 × 5 และพหุนาม ${\displaystyle x^{2}-4}$ สามารถแยกได้เป็น ${\displaystyle (x-2)(x+2)}$ เป็นต้นจำนวนเชิงซ้อน (อังกฤษ : complex number) ในทางคณิตศาสตร์ คือ เซตที่ต่อเติมจากเซตของจำนวนจริงโดยเพิ่มจำนวน ${\displaystyle i}$ ซึ่งทำให้สมการ ${\displaystyle i^{2}+1=0}$ เป็นจริง และหลังจากนั้นเพิ่มสมาชิกตัวอื่น ๆ เข้าไปจนกระทั่งเซตที่ได้ใหม่มีสมบัติการปิดภายใต้การบวกและการคูณ จำนวนเชิงซ้อน ${\displaystyle z}$ ทุกตัวสามารถเขียนอยู่ในรูป ${\displaystyle x+iy}$ โดยที่ ${\displaystyle x}$ และ ${\displaystyle y}$ เป็นจำนวนจริง โดยเราเรียก ${\displaystyle x}$ และ ${\displaystyle y}$ ว่าส่วนจริง (real part) และส่วนจินตภาพ (imaginary part) ของ ${\displaystyle z}$ ตามลำดับ

จุดมุ่งหมายของการแยกตัวประกอบคือการลดทอนวัตถุให้เล็กลง อาทิ จากจำนวนไปเป็นจำนวนเฉพาะ จากพหุนามไปเป็นพหุนามลดทอนไม่ได้ (irreducible polynomial) การแยกตัวประกอบจำนวนเต็มเป็นส่วนหนึ่งของทฤษฎีบทมูลฐานของเลขคณิต ส่วนการแยกตัวประกอบพหุนามเป็นส่วนหนึ่งของทฤษฎีบทมูลฐานของพีชคณิต สำหรับพหุนาม สิ่งที่ตรงข้ามกับการแยกตัวประกอบคือการกระจายพหุนาม (polynomial expansion) ซึ่งเป็นการคูณตัวประกอบทุกตัวเข้าด้วยกันเป็นพหุนามใหม่

การแยกตัวประกอบจำนวนเต็มสำหรับจำนวนขนาดใหญ่อาจกลายเป็นข้อปัญหาที่ยุ่งยาก ซึ่งไม่มีวิธีใดที่สามารถแยกตัวประกอบจำนวนขนาดใหญ่ได้อย่างรวดเร็ว แต่ความยุ่งยากนี้เป็นประโยชน์ต่อการรักษาความปลอดภัยในขั้นตอนวิธีของการเข้ารหัสลับแบบกุญแจอสมมาตร อย่างเช่น RSA

สำหรับการแยกตัวประกอบของเมทริกซ์เรียกว่า การแยกเมทริกซ์ (matrix decomposition) ซึ่งมีวิธีการที่เหมาะสมแตกต่างกันไปสำหรับเมทริกซ์นั้นๆ เช่น การแยกแบบคิวอาร์ (QR decomposition) เป็นต้น วิธีหลักอย่างหนึ่งที่นิยมคือการทำให้เป็นผลคูณของ เมทริกซ์เชิงตั้งฉาก (orthogonal matrix) หรือเมทริกซ์ยูนิแทรี (unitary matrix) กับเมทริกซ์แบบสามเหลี่ยม (triangular matrix)

อีกตัวอย่างหนึ่งของการแยกตัวประกอบคือการแยกฟังก์ชันให้กลายเป็นการประกอบฟังก์ชัน (function composition) กับฟังก์ชันอื่นโดยมีเงื่อนไขที่เจาะจง ตัวอย่างเงื่อนไขเช่น ฟังก์ชันทุกฟังก์ชันสามารถเขียนให้อยู่ในรูปของการประกอบของฟังก์ชันทั่วถึง (surjective function) กับฟังก์ชันหนึ่งต่อหนึ่ง (injective function) เป็นต้น

พหุนามกำลังสองใดๆ บนจำนวนเชิงซ้อน (คือพหุนามที่อยู่ในรูป ${\displaystyle ax^{2}+bx+c}$ เมื่อ ${\displaystyle a,b,c\in \mathbb {C} }$) สามารถแยกตัวประกอบให้เป็นนิพจน์ที่อยู่ในรูป ${\displaystyle a(x-\alpha )(x-\beta )\!}$ เมื่อ ${\displaystyle \alpha }$ และ ${\displaystyle \beta }$ คือรากของพหุนาม ซึ่งคำนวณได้จากสูตรกำลังสองดังนี้

${\displaystyle ax^{2}+bx+c=a(x-\alpha )(x-\beta )=a\left(x-\left({\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\right)\left(x-\left({\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right)\right)}$

บางครั้งพหุนามกำลังสองสามารถแยกออกได้เป็นทวินาม (binomial) สองตัวด้วยสัมประสิทธิ์ที่เป็นจำนวนเต็ม โดยไม่จำเป็นต้องใช้สูตรกำลังสองในการคำนวณ ซึ่งมีประโยชน์สำหรับการหารากของสมการกำลังสอง โดยที่พหุนาม

${\displaystyle ax^{2}+bx+c\!}$

สามารถแยกได้เป็น

${\displaystyle (mx+p)(nx+q)\!}$

เมื่อ

${\displaystyle mn=a\!}$

${\displaystyle pq=c\!}$

${\displaystyle pn+mq=b\!}$

จากนั้นจึงให้ทวินามแต่ละตัวเท่ากับศูนย์ แล้วคำนวณหาค่าของ x เพื่อหารากของสมการกำลังสอง

พหุนามกำลังสองบางชนิดสามารถแยกตัวประกอบออกได้เป็นทวินามที่เหมือนกัน พหุนามนั้นเรียกว่า ไตรนามกำลังสองสมบูรณ์ หรือเพียงแค่ กำลังสองสมบูรณ์ ซึ่งพหุนามดังกล่าวสามารถแยกได้ดังนี้

${\displaystyle (a+b)^{2}=(a+b)(a+b)=a^{2}+2ab+b^{2}}$

${\displaystyle (a-b)^{2}=(a-b)(a-b)=a^{2}-2ab+b^{2}}$

การแยกตัวประกอบทางพีชคณิตอีกอย่างหนึ่งเรียกว่า ผลต่างกำลังสอง มีสูตรดังนี้

${\displaystyle a^{2}-b^{2}=(a-b)(a+b)\!}$

ซึ่งเป็นจริงสำหรับทั้งสองพจน์ ไม่ว่าจำนวนเหล่านั้นจะเป็นกำลังสองสมบูรณ์หรือไม่ ถ้าพจน์ทั้งสองลบกัน ก็ให้แทนด้วยสูตรดังกล่าวได้ทันที แต่ถ้าพจน์ทั้งสองบวกกัน ทวินามที่ได้จากการแยกตัวประกอบจะต้องมีจำนวนจินตภาพเข้ามาเกี่ยวข้อง ซึ่งแสดงได้ดังนี้

${\displaystyle a^{2}+b^{2}=(a+bi)(a-bi)\!}$

ตัวอย่างเช่น ${\displaystyle 4x^{2}+49}$ สามารถแยกได้เป็น ${\displaystyle (2x+7i)(2x-7i)}$ เป็นต้น

สูตรสำหรับการแยกตัวประกอบของผลบวกและผลต่างกำลังสามเป็นดังนี้ ผลบวกและผลต่างสามารถแยกตัวประกอบเป็น

${\displaystyle a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\!}$

${\displaystyle a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\!}$

เช่น x³ − 10³ (or x³ − 1000) สามารถแยกตัวประกอบเป็น (x − 10)(x² + 10x + 100)