บทนำทฤษฎีสัมพัทธภาพทั่วไป

บทความนี้อ้างอิงคริสต์ศักราช/คริสต์ทศวรรษ/คริสต์ศตวรรษ ซึ่งเป็นสาระสำคัญของเนื้อหา

ทฤษฎีสัมพัทธภาพทั่วไป เป็นทฤษฎีความโน้มถ่วงซึ่งอัลเบิร์ต ไอน์สไตน์พัฒนาระหว่างปี 1907 ถึง 1915 มีใจความว่า ผลของความโน้มถ่วงที่สังเกตได้ระหว่างมวลเกิดจากการบิดงอ (warp) ของปริภูมิ-เวลา

ต้นคริสต์ศตวรรษที่ 20 กฎความโน้มถ่วงสากลของนิวตันเป็นที่ยอมรับกันมานานกว่าสองร้อยปีว่าเป็นคำอธิบายแรงโน้มถ่วงระหว่างมวลที่สมเหตุสมผล ในแบบจำลองของนิวตัน ความโน้มถ่วงเป็นผลของแรงดึงดูดระหว่างวัตถุฟากฟ้าขนาดมหึมา แม้นิวตันประสบปัญหาจากธรรมชาติที่ยังไม่ทราบของแรงนั้น แต่ทฤษฎีแรงโน้มถ่วงของนิวตันกลายมาเป็นกรอบพื้นฐานที่ประสบความสำเร็จอย่างยิ่งในการอธิบายการเคลื่อนที่ของวัตถุฟากฟ้า

การทดลองและการสังเกตแสดงว่าคำอธิบายความโน้มถ่วงของไอน์สไตน์อธิบายหลายปรากฏการณ์ที่กฎของนิวตันไม่อธิบาย เช่น ค่าผิดปกติเล็กน้อยในวงโคจรของดาวพุธและดาวเคราะห์อื่น สัมพัทธภาพทั่วไปยังทำนายผลใหม่ของความโน้มถ่วง เช่น คลื่นความโน้มถ่วง เลนส์ความโน้มถ่วง และผลของความโน้มถ่วงต่อเวลาที่เรียก การขยายขนาดของเวลาจากความโน้มถ่วง (gravitational time dilation) การทำนายเหล่านี้จำนวนมากได้รับการยืนยันจากการทดลองหรือการสังเกต ล่าสุดได้แก่ คลื่นความโน้มถ่วง ส่วนการทำนายอื่น ๆ เป็นหัวข้อการวิจัยที่กำลังดำเนินอยู่

มีการพัฒนาสัมพัทธภาพทั่วไปเป็นเครื่องมือสำคัญในฟิสิกส์ดาราศาสตร์สมัยใหม่ โดยเป็นรากฐานของความเข้าใจปัจจุบันของหลุมดำ ซึ่งเป็นบริเวณของปริภูมิซึ่งผลความโน้มถ่วงเข้มเสียจนแม้แต่แสงก็ออกมาไม่ได้ ความโน้มถ่วงที่เข้มของหลุมดำคาดว่าทำให้เกิดการปล่อยรังสีอย่างเข้มโดยวัตถุทางดาราศาสตร์บางชนิด (เช่น นิวเคลียสดาราจักรกัมมันต์หรือไมโครควาซาร์) สัมพัทธภาพทั่วไปยังเป็นส่วนหนึ่งของกรอบแบบจำลองจักรวาลวิทยาบิกแบงมาตรฐาน

แม้สัมพัทธภาพทั่วไปมิใช่ทฤษฎีความโน้มถ่วงสัมพัทธนิยมทฤษฎีเดียว แต่เป็นทฤษฎีที่เรียบง่ายที่สุดซึ่งเข้ากันกับข้อมูลการทดลอง กระนั้น ยังมีคำถามที่ไม่มีคำตอบอยู่จำนวนหนึ่ง คำถามหลักมูลที่สุดคือ สัมพัทธภาพทั่วไปจะสามารถเข้าได้กับกฎกลศาสตร์ควอนตัมได้อย่างไรเพื่อผลิตทฤษฎีความโน้มถ่วงเชิงควอนตัมที่สมบูรณ์และต้องกันในตนเอง

ในเดือนกันยายน 1905 อัลเบิร์ต ไอน์สไตน์จัดพิมพ์ทฤษฎีสัมพัทธภาพพิเศษของตน ซึ่งทำให้กฎการเคลื่อนที่ของนิวตันเข้าได้กับไฟฟ้าพลศาสตร์ (อันตรกิริยาระหว่างวัตถุกับประจุไฟฟ้า) สัมพัทธภาพพิเศษนำกรอบใหม่มาให้วิชาฟิสิกส์ทั้งหมดโดยเสนอมโนทัศน์ใหม่ปริภูมิและเวลา ทฤษฎีฟิสิกส์ซึ่งเป็นที่ยอมรับกันในเวลานั้นบางทฤษฎีไม่ต้องกันกับกรอบนั้น ตัวอย่างสำคัญคือ ทฤษฎีความโน้มถ่วงของนิวตันซึ่งอธิบายความดึงดูดระหว่างกันระหว่างวัตถุอันเนื่องจากมวลของมัน

นักฟิสิกส์หลายคนรวมทั้งไอน์สไตน์ค้นหาทฤษฎีซึ่งจะทำให้กฎความโน้มถ่วงของนิวตันเข้าได้กับทฤษฎีสัมพัทธภาพพิเศษ มีเพียงทฤษฎีของไอน์สไตน์เท่านั้นที่ได้รับการพิสูจน์แล้วว่าสอดคล้องกับการทดลองและการสังเกต เพื่อเข้าใจความคิดพื้นฐานของทฤษฎี ในการนี้การติดตามความคิดของไอน์สไตน์ระหว่างปี 1907 ถึง 1915 จะให้รายละเอียด ตั้งแต่การทดลองทางความคิดเบื้องต้นของเขาอันเกี่ยวข้องกับผู้สังเกตในการตกอิสระสู่ทฤษฎีความโน้มถ่วงเรขาคณิตสมบูรณ์ของเขา^[1]

บุคคลในลิฟต์ที่ตกอย่างอิสระประสบภาวะไร้น้ำหนัก วัตถุจะลอยอยู่โดยไร้การเคลื่อนไหวหรือเคลื่อนไหวด้วยความเร็วคงที่ เนื่องจากทุกสิ่งในลิฟต์ตกลงไปด้วยกัน จึงไม่สามารถสังเกตผลของความโน้มถ่วงได้ ด้วยวิธีนี้ประสบการณ์ของผู้สังเกตในการตกอย่างอิสระจึงแยกไม่ได้กับผู้สังเกตในอวกาศซึ่งอยู่ห่างจากแหล่งความโน้มถ่วงสำคัญใด ๆ ผู้สังเกตเหล่านั้นเป็นผู้สังเกตเฉื่อยที่ไอน์สไตน์อธิบายไว้ในทฤษฎีสัมพัทธภาพพิเศษของเขา คือ ผู้สังเกตซึ่งแสงเดินทางเป็นเส้นตรงด้วยความเร็วคงที่^[2]

ไอน์สไตน์ตั้งสมมติฐานว่าประสบการณ์คล้ายกันของผู้สังเกตไร้น้ำหนักและผู้สังเกตเฉื่อยในทฤษฎีสัมพัทธภาพพิเศษเป็นตัวแทนของคุณสมบัติมูลฐานของความโน้มถ่วง และเขายกให้ข้อนี้เป็นหลักหมุดของทฤษฎีสัมพัทธภาพทั่วไปของเขา โดยสรุปไว้ในหลักการสมมูลของเขา กล่าวโดยคร่าว ๆ คือ หลักการนี้ระบุว่าบุคคลในลิฟต์ที่ตกอย่างอิสระไม่สามารถบอกได้ว่าตนกำลังตกอย่างอิสระ ทุกการทดลองที่มีสิ่งแวดล้อมตกอย่างอิสระดังนี้ให้ผลลัพธ์เช่นเดียวกับผู้สังเกตขณะพักหรือกำลังเคลื่อนที่เป็นระเบียบในอวกาศที่อยู่ห่างจากแหล่งความโน้มถ่วงใด ๆ^[3]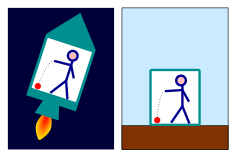

ผลของความโน้มถ่วงส่วนใหญ่หายไปเมื่ออยู่ในการตกอย่างอิสระ แต่ผลที่ดูเหมือนผลของความโน้มถ่วงนั้นสามารถทำให้เกิดได้ในกรอบอ้างอิงเร่ง (accelerated frame of reference) ผู้สังเกตในห้องปิดไม่สามารถแยกแยะได้ว่าสองกรณีด้านล่างกรณีใดเป็นจริง

1. วัตถุกำลังตกสู่พื้น เพราะห้องนั้นกำลังอยู่บนผิวโลกและวัตถุนั้นกำลังถูกความโน้มถ่วงดึงลงมา
2. วัตถุกำลังตกสู่พื้น เพราะห้องนั้นอยู่บนจรวดในอวกาศ ซึ่งมีความเร่ง 9.81 m/s² และอยู่ห่างจากแหล่งกำเนิดความโน้มถ่วงใด ๆ วัตถุนั้นกำลังถูกดึงลงพื้นด้วย "แรงเฉื่อย" เดียวกันกับที่ผลักผู้ขับรถที่มีความเร่งไปชนกับเบาะที่นั่งด้านหลังบุคคลนั้น

ในทางกลับกัน ผลใด ๆ ที่สังเกตได้ในกรอบอ้างอิงเร่งควรสังเกตได้ในสนามความโน้มถ่วงที่มีความเข้มพอ ๆ กันได้เช่นกัน หลักการนี้ทำให้ไอน์สไตน์สามารถพยากรณ์ผลของความโน้มถ่วงใหม่ ๆ หลายประการได้ในปี 1907 ดังที่จะอธิบายในส่วนถัดไป

ผู้สังเกตในกรอบอ้างอิงเร่งจะต้องใช้สิ่งที่นักฟิสิกส์เรียกว่า แรงเทียม เพื่อใช้อธิบายความเร่งที่เขาและวัตถุรอบตัวเขาประสบ ตัวอย่างหนึ่งเช่น แรงที่ผลักผู้ขับรถที่มีความเร่งไปยังเบาะนั่งด้านหลังบุคคลนั้นดังที่ได้กล่าวไปแล้ว อีกตัวอย่างหนึ่งคือแรงที่บุคคลรู้สึกว่ากำลังดึงแขนขึ้นและออกจากตัวเมื่อกำลังพยายามหมุนเหมือนลูกข่าง วิจารณญาณของไอน์สไตน์มีว่า โดยหลักพื้นฐานแล้วแรงดึงซึ่งคงที่และเคยชินของสนามความโน้มถ่วงของโลกก็เป็นเฉกเช่นแรงเทียมเหล่านี้^[4] ขนาดปรากฏของแรงเทียมดูเหมือนเป็นสัดส่วนกับมวลของวัตถุใด ๆ ที่แรงนั้นกระทำเสมอ ตัวอย่างเช่น เบาะนั่งของผู้ขับส่งแรงเพียงพอให้เร่งผู้ขับในอัตราเดียวกับรถยนต์นั้น ไอน์สไตน์จึงเสนอว่าวัตถุในสนามความโน้มถ่วงควรได้รับแรงความโน้มถ่วงเป็นสัดส่วนกับมวลของมัน ดังที่กล่าวไว้ในกฎความโน้มถ่วงของนิวตัน^[5]

ในปี 1907 ก่อนไอน์สไตน์คิดค้นทฤษฎีสัมพัทธภาพทั่วไปเสร็จสิ้นแปดปี กระนั้น เขาสามารถพยากรณ์แบบใหม่ที่ทดสอบได้ซึ่งอาศัยจุดตั้งต้นสำหรับพัฒนาทฤษฎีใหม่ของเขา คือ หลักการสมมูล^[6]

ผลใหม่อย่างแรก คือ การเลื่อนความถี่เชิงโน้มถ่วงของแสง พิจารณาผู้สังเกตสองคนบนยานจรวดที่มีความเร่ง บนยานดังกล่าวมีมโนทัศน์ธรรมชาติ "ขึ้น" และ "ลง" อยู่ โดยทิศทางที่ยานเร่งไปนั้นเรียก "ขึ้น" และวัตถุที่ไม่ถูกผูกยึดจะเร่งไปในทิศทางตรงข้าม หรือตก "ไปด้านล่าง" สันนิษฐานว่าผู้สังเกตคนหนึ่งอยู่ "สูงกว่า" อีกคนหนึ่ง เมื่อผู้สังเกตคนที่อยู่ต่ำกว่าส่งสัญญาณแสงแก่ผู้สังเกตที่อยู่สูงกว่า ความเร่งจะทำให้แสงเลื่อนไปทางแดงซึ่งตรงกับที่อาจคำนวณได้จากสัมพัทธภาพพิเศษ ผู้สังเกตคนที่สองจะวัดได้แสงความถี่ต่ำกว่าผู้สังเกตคนแรก ในทางกลับกัน แสงที่ส่งจากผู้สังเกตที่อยู่สูงกว่าจะเลื่อนไปทางน้ำเงิน คือ เลื่อนไปยังความถี่สูงขึ้น^[7] ไอน์สไตน์แย้งว่าการเลื่อนของความถี่ดังกล่าวจะต้องสังเกตได้ในสนามความโน้มถ่วงเช่นกัน ปรากฏการณ์ดังกล่าวพรรณนาในภาพด้านซ้ายมือ ซึ่งแสดงคลื่นแสงที่ค่อย ๆ เลื่อนไปทางแดงดังเช่นที่แสงประพฤติระหว่างเคลื่อนที่ขึ้นบนต่อความเร่งของความโน้มถ่วง ผลนี้มีการยืนยันในการทดลองแล้วดังอธิบายด้านล่าง

การเลื่อนความถี่จากความโน้มถ่วงนี้สมนัยกับการขยายขนาดของเวลาจากความโน้มถ่วง เนื่องจากผู้สังเกต "ที่อยู่สูงกว่า" วัดคลื่นแสงเดียวกันมีความถี่ต่ำกว่าผู้สังเกตที่อยู่ "ต่ำกว่า" เวลาจะต้องผ่านไปเร็วกว่าสำหรับผู้สังเกตที่อยู่สูงกว่าด้วย ฉะนั้น เวลาจึงผ่านไปช้ากว่าสำหรับผู้สังเกตที่อยู่ต่ำกว่าในสนามความโน้มถ่วง

สำคัญที่ต้องเน้นย้ำว่าสำหรับผู้สังเกตแต่ละคน ไม่มีการเปลี่ยนแปลงการไหลของเวลาที่สังเกตได้สำหรับเหตุการณ์หรือกระบวนการซึ่งเป็นขณะพักในกรอบอ้างอิงของผู้สังเกตนั้น ไข่ห้านาทีที่จับเวลาด้วยนาฬิกาของผู้สังเกตแต่ละคนจะมีเนื้ออย่างเดียวกัน เมื่อเวลาผ่านไปหนึ่งปีตามเวลาทั้งสองเรือน ผู้สังเกตทั้งสองจะมีอายุมากขึ้นตามเวลานั้นด้วย กล่าวสั้น ๆ คือ นาฬิกาแต่ละเรือนสอดคล้องอย่างไร้ที่ติกับกระบวนการทั้งหมดที่เกิดขึ้นในบริเวณใกล้เคียงของนาฬิกานั้น จะสามารถสังเกตว่าเวลาสำหรับผู้สังเกตที่อยู่ต่ำกว่าเดินช้ากว่าผู้สังเกตที่อยู่สูงกว่าเฉพาะเมื่อมีการเปรียบเทียบนาฬิการะหว่างผู้สังเกตหลายคนเท่านั้น^[8] ผลนี้เล็กน้อยมาก แต่ก็มีการยื่นยันแล้วในการทดลองหลายครั้ง ดังอธิบายด้านล่าง

ในทำนองเดียวกัน ไอน์สไตน์พยากรณ์การเบนแสงจากความโน้มถ่วง กล่าวคือ ในสนามความโน้มถ่วง แสงถูกเบนไปในทิศทางลง ในทางปริมาณ ผลเฉลยของไอน์สไตน์คลาดเคลื่อนไปสองเท่า การแปลงที่ถูกต้องต้องอาศัยสูตรที่มีความสมบูรณ์มากขึ้นจากทฤษฎีสัมพัทธภาพทั่วไป ไม่เพียงอาศัยเฉพาะหลักการสมมูล^[9]

ความสมมูลระหว่างผลความโน้มถ่วงและความเฉื่อยไม่เป็นส่วนหนึ่งของทฤษฎีความโน้มถ่วงที่สมบูรณ์ เมื่อต้องใช้อธิบายความโน้มถ่วงใกล้ตำแหน่งของบุคคลบนผิวโลก สังเกตว่ากรอบอ้างอิงของบุคคลนั้นไม่ใช่การตกอย่างอิสระ ฉะนั้นจึงคาดว่าจะมีแรงเสียดทาน จะให้คำอธิบายที่เหมาะสม แต่กรอบอ้างอิงการตกอิสระบนฝั่งหนึ่งของโลกไม่สามารถอธิบายได้ว่าเหตุใดบุคคลที่อยู่ฝั่งตรงข้ามของโลกถูกแรงโน้มถ่วงดึงในทิศทางตรงกันข้าม

หากจะอธิบายให้ง่ายขึ้น แรงเดียวกันนี้ยังปรากฏในเทห์ฟ้าสองเทห์ซึ่งตกลงสู่ลงเคียงกัน ในกรอบอ้างอิงซึ่งเป็นการตกอิสระข้างเทห์ทั้งสองนี้ จะดูเหมือนว่าทั้งสองจะลอยอยู่โดยไร้น้ำหนัก แต่แท้จริงแล้วไม่ใช่ เทห์ทั้งสองนี้ไม่ได้ตกลงในทิศทางเดียวกันพอดี แต่ตกลงสู่จุดจุดหนึ่งในปริภูมิ กล่าวคือ ศูนย์กลางความโน้มถ่วงของโลก ผลทำให้การเคลื่อนที่ของเทห์แต่ละเทห์บางส่วนเคลื่อนที่เข้าหากัน ในสิ่งแวดล้อมขนาดเล็ก เช่น ลิฟต์ที่ตกอย่างอิสระ ความเร่งโดยสัมพัทธ์นี้มีค่าเล็กน้อยมาก แต่นักดิ่งพสุธาที่อยู่ฝั่งตรงข้ามของโลก ผลนี้จะมีค่ามาก ผลต่างของแรงดังนี้ยังมีส่วนให้เกิดน้ำขึ้นลงในมหาสมุทร ปรากฏการณ์นี้จึงได้ชื่อว่า "ผลน้ำขึ้นลง"

ความสมมูลระหว่างความเฉื่อยและควาามโน้มถ่วงไม่สามารถอธิบายผลน้ำขึ้นลงได้ ไม่สามารถความผันแปรในสนามความโน้มถ่วงนี้ หากจะอธิบายความผันแปรในสนามโน่มถ่วง^[10] จำเป็นต้องมีทฤษฎีซึ่งอธิบายวิธีที่สสาร (เช่น มวลใหญ่อย่างโลก) มีผลต่อสิ่งแวดล้อมเฉื่อยโดยรอบมวลนั้น

ในการสำรวจความสมมูลของความโน้มถ่วงและความเร่งตลอดจนบทบาทของแรงน้ำขึ้นลง ไอน์สไตน์ค้นพบแนวเทียบหลายอย่างกับเรขาคณิตผิว ตัวอย่างได้แก่การเปลี่ยนผ่านจากกรอบอ้างอิงเฉื่อย (ซึ่งอนุภาคอิสระวิ่งด้วยแรงเฉื่อยตามวิถีเส้นตรง ณ ความเร็วคงที่) ไปเป็นกรอบอ้างอิงหมุน (ซึ่งจำเป็นต้องคิดพจน์เพิ่มเติมที่สมนัยกับแรงเสียดทานเพื่ออธิบายการเคลื่อนที่ของอนุภาค) นี่เป็นแนวเทียบการเปลี่ยนผ่านจากระบบพิกัดคาร์ทีเซียน (ซึ่งเส้นพิกัดเป็นเส้นตรง) เป็นระบบพิกัดเชิงเส้นโค้ง (ซึ่งเส้นพิกัดไม่จำเป็นต้องเป็นเส้นตรง)

แนวเทียบที่ลึกกว่าเกี่ยวข้องกับแรงน้ำขึ้นลงทีมีคุณสมบัติของพื้นผิวเรียกความโค้ง สำหรับสนามความโน้มถ่วง การมีหรือไม่มีแรงน้ำขึ้นลงตัดสินว่าอิทธิพลของความโน้มถ่วงสามารถกำจัดได้ด้วยการเลือกกรอบอ้างอิงการตกอย่างอิสระหรือไม่ ในทำนองเดียวกัน การมีหรือไม่มีความโค้งตัดสินว่าพื้นผิวนั้นเทียบเท่ากับระนาบหนึ่งหรือไม่ ในฤดูร้อนปี 1912 ไอน์สไตน์ได้รับบันดาลใจจากแนวเทียบเหล่านี้ และค้นหาการบัญญัติความโน้มถ่วงแบบเรขาคณิต^[11]

วัตถุมูลฐานในวิชาเรขาคณิตซึ่งได้แก่ จุด เส้นตรง และสามเหลี่ยม เดิมนิยามในปริภูมิสามมิติหรือในผิวสองมิติ ในปี 1907 แฮร์มัน มิงค็อฟสกี อดีตศาตราจารย์คณิตศาสตร์ของไอน์สไตน์ที่พอลิเทคนิคกลางสวิส ริเริ่มการคิดค้นทางเรขาคณิตซึ่งทฤษฎีสัมพัทธภาพพิเศษของไอน์สไตน์โดยที่เรขาคณิตนั้นไม่คิดเฉพาะปริภูมิเท่านั้นแต่คิดเวลาด้วย เอนทิตีพื้นฐานของเรขาคณิตใหม่นี้ คือ ปริภูมิ-เวลาสี่มิติ วงโคจรของเทห์ที่เคลื่อนที่เป็นเส้นโค้งในปริภูมิ-เวลา วงโคจรของเทห์ที่เคลื่อนที่ด้วยความเร็วคงที่โดยไม่เปลี่ยนทิศทางสมนัยกับเส้นตรง^[12]

สำหรับพื้นผิว การวางนัยทั่วไปจากเรขาคณิตของระนาบหรือพื้นผิวเรียบไปเป็นพื้นผิวโค้งโดยทั่วไปมีการอธิบายในต้นคริสต์ศตวรรษที่ 19 โดยคาร์ล ฟรีดริช เกาส์ คำบรรยายนี้มีการวางนัยทั่วไปไปยังปริภูมิที่มีมติสูงกว่าในรูปนัยนิยมทางคณิตศาสตร์ที่แบร์นฮาร์ท รีมันเผยแพร่ในคริสต์ทศวรรษ 1850 ด้วยความช่วยเหลือของเรขาคณิตแบบรีมัน ไอน์สไตน์บัญญัติคำบรรยายความโน้มถ่วงทางเรขาคณิตโดยที่ปริภูมิ-เวลาของมิงค็อฟสกีถูกแทนที่ด้วยปริภูมิ-เวลาโค้งบิดเบี้ยว เช่นเดียวกับที่พื้นผิวโค้งเป็นนัยทั่วไปของพื้นผิวระนาบธรรมดา มีการใช้ระนาบฝังตัว (Embedding Diagram) เพื่อพรรณนาปริภูมิ-เวลาโค้งในบริบทการศึกษา^[13][14]

หลังไอน์สไตน์ทราบความสมเหตุสมผลของแนวเทียบเรขาคณิตดังนี้แล้ว ไอน์สไตน์ยังต้องใช้เวลาอีกสามปีจึงค้นพบหินหลักมุมที่หายไปสำหรับทฤษฎีของเขา นั่นคือ สมการอธิบายว่าสสารมีอิทธิพลต่อความโค้งของปริภูมิ-เวลาอย่างไร หลังบัญญัติสมการที่ปัจจุบันเรียก สมการของไอน์สไตน์ (หรือจะกล่าวให้แม่นยำยิ่งขึ้นว่าสมการสนามของไอน์สไตน์) แล้ว เขานำเสนอทฤษฎีความโน้มถ่วงใหม่นี้ในสมัยประชุมหลายสมัยของวิทยาลัยวิทยาศาสตร์ปรัสเซียในปลายปี 1915 จนนำไปสู่การนำเสนอสุดท้ายของเขาในวันที่ 25 พฤศจิกายน 1915^[15]

ทฤษฎีสัมพัทธภาพเชิงเรขาคณิตของไอน์สไตน์สรุปได้โดยถอดความจากจอห์น วีลเลอร์ (John Wheeler) ดังนี้ ปริภูมิ-เวลาบอกวิธีเคลื่อนที่แก่สสาร สสารบอกวิธีโค้งแก่ปริภูมิ-เวลา^[16] ความหมายของประโยคนี้มีการกล่าวถึงในสามส่วนนับจากนี้ ซึ่งสำรวจการเคลื่อนที่ของสิ่งที่เรียกอนุภาคทดสอบ ตรวจสอบว่าคุณสมบัติใดของสสารเป็นบ่อเกิดของความโน้มถ่วง และสุดท้ายนำเสนอสมการของไอน์สไตน์ ซึ่งโยงคุณสมบัติของสสารเหล่านี้เข้ากับความโค้งของปริภูมิ-เวลา

ในการทำแผนที่อิทธิพลความโน้มถ่วงของเทห์ (body) จะมีประโยชน์หากคิดถึงสิ่งที่นักฟิสิกส์เรียกโพรบ (probe) หรืออนุภาคทดสอบ คือ อนุภาคที่ได้รับอิทธิพลจากความโน้มถ่วง แต่ยังเล็กและเบาจนไม่ต้องสนใจผลความโน้มถ่วงของมันเอง เมื่อปราศจากความโน้มถ่วงและแรงภายนอกอื่น อนุภาคทดสอบเคลื่อนเป็นเส้นตรงด้วยความเร็วคงที่ ในภาษาปริภูมิ-เวลา การเคลื่อนที่นี้เทียบเท่าการกล่าวว่าอนุภาคทดสอบเคลื่อนที่ตามเวิลด์ไลน์ (world line) ตรงในปริภูมิ-เวลา เมื่อมีความโน้มถ่วง ปริภูมิ-เวลาเป็นนอกแบบยูคลิดหรือมีความโค้ง และในปริภูมิ-เวลาโค้งอาจไม่มีเวิลด์ไลน์ตรงอยู่ แต่อนุภาคทดสอบเคลื่อนที่ตามแนวเรียก จีออเดสิก (geodesic) ที่ "ตรงเท่าที่เป็นไปได้" นั่นคือ แนวนี้ตามวิถีสั้นสุดระหว่างจุดเริ่มต้นและสิ้นสุด เมื่อพิจารณาความโค้งด้วย

อุปมาง่าย ๆ ดังนี้ ในวิชาภูมิมาตรศาสตร์ วิทยาศาสตร์การวัดขนาดและรูปทรงของโลก จีออเดสิก (geodesic, มาจากภาษากรีก "geo" แปลว่า โลก และ "daiein" แปลว่า แบ่ง) คือ เส้นทางสั้นสุดระหว่างสองจุดบนผิวโลก เส้นทางนี้โดยประมาณก็คือเซกเมนต์หนึ่งของวงกลมใหญ่ เช่น เส้นลองจิจูดหรือเส้นศูนย์สูตร แน่นอนว่าวิถีเหล่านี้มิใช่เส้นตรง เพราะเส้นต้องไปตามความโค้งของผิวโลก แต่เส้นเหล่านี้ตรงเท่าที่เป็นไปได้ในเงื่อนไขบังคับนี้

คุณสมบัติภูมิมาตรศาสตร์ต่างจากคุณสมบัติของเส้นตรง ตัวอย่างเช่น ในระนาบหนึ่ง เส้นขนานจะไม่มีทางมาบรรจบกัน แต่ไม่จริงสำหรับจีออเดสิกบนผิวโลก ตัวอย่างเช่น เส้นลองจิจูดขนานที่เส้นศูนย์สูตร แต่มีส่วนร่วมที่ขั้ว ทำนองเดียวกัน เวิลด์ไลน์ของอนุภาคทดสอบในการตกอย่างอิสระเป็นจีออเดสิกของปริภูมิ-เวลาหรือเป็นเส้นตรงที่สุดที่เป็นไปได้ในปริภูมิ-เวลา แต่ยังมีข้อแตกต่างสำคัญระหว่างทั้งสองและเส้นตรงจริง ๆ เท่านั้นที่สามารถวาดได้ในปริภูมิ-เวลาไร้ความโน้มถ่วงของสัมพัทธภาพพิเศษ ในสัมพัทธภาพพิเศษ จีออเดสิกขนานยังขนานกันอยู่ ในสนามความโน้มถ่วงที่มีผลน้ำขึ้นลง โดยทั่วไปข้อนี้จะไม่เป็นจริง ตัวอย่างเช่น หากวัตถุสองวัตถุที่ทีแรกอยู่ในภาวะพักโดยสัมพัทธ์ต่อกัน แต่แล้วถูกปล่อยในสนามความโน้มถ่วงของโลก วัตถุทั้งสองจะเคลื่อนเข้าหากันขณะที่ตกสู่ศูนย์กลางของโลก^[17]

วัตถุในชีวิตประจำวัน (คน รถยนต์ บ้านหรือแม้แต่ภูเขา) มีมวลน้อยนิดเมื่อเทียบกับดาวเคราะห์หรือเทห์ดาราศาสตร์อื่น เมื่อกล่าวถึงวัตถุในชีวิตประจำวัน กฎว่าด้วยพฤติกรรมของอนุภาคทดสอบเพียงพออธิบายสิ่งที่เกิด ที่สำคัญคือ ในการเบนอนุภาคทดสอบจากวิถีจีออเดสิกของมันจะต้องมีแรงภายนอกมากระทำ เก้าอี้ที่มีผู้นั่งอยู่มีแรงพุ่งขึ้นภายนอกมากระทำป้องกันมิให้บุคคลนั้นตกอิสระสู่ศูนย์กลางของโลกฉะนั้นจึงเป็นไปตามจีออเดสิก ซึ่งหากไม่มีสสารกั้นระหว่างเขากับศูนย์กลางของโลกเขาก็จะตกลงเบื้องล่าง ด้วยวิธีนี้ สัมพัทธภาพทั่วไปอธิบายประสบการณ์แรงโน้มถ่วงประจำวันบนผิวโลกว่ามิใช่เป็นแรงดึงลงของแรงโน้มถ่วง แต่เป็นการผลักขึ้นของแรงภายนอก แรงเหล่านี้เบนเทห์ทั้งหมดที่อยู่บนผิวโลกจากจีออเดสิกที่ควรเป็นตามปกติ^[18] สำหรับวัตถุสสารซึ่งต้องคิดอิทธิพลความโน้มถ่วงของมันด้วย กฎการเคลื่อนที่จะซับซ้อนกว่าของอนุภาคทดสอบอยู่บ้าง แต่ข้อที่ว่าปริภูมิ-เวลาบอกวิธีเคลื่อนที่แก่สสารยังเป็นจริงอยู่^[19]

ในคำอธิบายความโน้มถ่วงของนิวตัน แรงโน้มถ่วงเกิดจากสสาร หรือจะกล่าวให้แม่นตรงกว่านั้น เกิดจากคุณสมบัติเฉพาะหนึ่งของวัตถุกายภาพ คือ มวล ในทฤษฎีของไอน์สไตน์และทฤษฎีความโน้มถ่วงที่สัมพันธ์กัน ความโค้งทุกจุดในปริภูมิ-เวลาก็เกิดจากว่ามีสสารอะไรอยู่ ซึ่งในที่นี้มวลเป็นคุณสมบัติสำคัญเช่นเดียวกันในการกำหนดอิทธิพลความโน้มถ่วงของสสาร แต่ในทฤษฎีความโน้มถ่วงสัมพัทธนิยม มวลไม่สามารถเป็นแหล่งของความโน้มถ่วงเพียงแหล่งเดียว สัมพัทธภาพโยงมวลกับพลังงาน และพลังงานกับโมเมนตัม

ความสมมูลระหว่างมวลกับพลังงาน ดังที่แสดงโดยสูตร E = mc² เป็นผลลัพธ์ที่โด่งดังที่สุดของสัมพัทธภาพพิเศษ ในสัมพัทธภาพ มวลและพลังงานเป็นวิธีการอธิบายปริมาณทางกายภาพหนึ่ง ๆ ที่ต่างกันสองวิธี หากระบบกายภาพหนึ่งมีพลังงาน ระบบนั้นจะมีมวลสมนัย และระบบกายภาพที่มีมวลก็จะมีพลังงานสมนัยด้วย โดยเฉพาะอย่างยิ่ง คุณสมบัติทั้งหมดของเทห์ที่สัมพันธ์กับพลังงาน เช่น อุณหภูมิหรือพลังงานยึดเหนี่ยวของระบบ เช่น นิวเคลียสหรือโมเลกุล ประกอบเป็นมวลของเทห์นั้น ฉะนั้นจึงประพฤติตนเป็นแหล่งของความโน้มถ่วง^[20]

ในสัมพัทธภาพพิเศษ พลังงานมีความเชื่อมโยงใกล้ชิดกับโมเมนตัม ดังเช่นที่ปริภูมิและเวลาในทฤษฎีนั้นต่างเป็นส่วนหนึ่งของเอนทิตีครอบคลุมกว่าที่เรียก ปริภูมิ-เวลา พลังงานและโมเมนตัมเป็นเพียงส่วนหนึ่งในปริมาณสี่มิติรวมที่นักฟิสิกส์เรียก สี่โมเมนตัม (four-momentum) ผลคือ หากพลังงานเป็นแหล่งของความโน้มถ่วง โมเมนตัมก็เป็นแหล่งด้วย ข้อนี้เป็นจริงสำหรับปริมาณที่เกี่ยวข้องโดยตรงกับพลังงานและโมเมนตัม กล่าวคือ ความดันภายในและความตึง เมื่อคิดรวมกัน ในสัมพัทธภาพทั่วไป มวล พลังงาน โมเมนตัม ความดันและความตึงเป็นแหล่งของความโน้มถ่วง เป็นวิธีที่สสารบอกปริภูมิ-เวลาว่าจะโค้งอย่างไร ในการบัญญัติทางคณิตศาสตร์ของทฤษฎี ปริมาณเหล่านี้ทั้งหมดเป็นส่วนหนึ่งของปริมาณทางกายภาพครอบคลุมกว่าที่เรียก เทนเซอร์พลังงาน–โมเมนตัม (energy–momentum tensor)^[21]

สมการของไอน์สไตน์เป็นหัวใจของสัมพัทธภาพทั่วไป สมการเหล่านี้ให้ประมวลความสัมพันธ์ระหะว่างเรขาคณิตปริภูมิ-เวลาและคุณสมบัติของสสารที่แม่นยำโดยใช้ภาษาคณิตศาสตร์ ที่เป็นรูปธรรมกว่านั้น มีการประมวลสูตรเหล่านี้โดยใช้มโนทัศน์เรขาคณิตรีมันน์ ซึ่งคุณสมสบัติเรขาคณิตของปริภูมิ (หรือปริภูมิ-เวลา) อธิบายโดยคุณสมบัติที่เรียกว่า เมตริก (metric) เมตริกเข้ารหัสสารสนเทศที่จำเป็นต้องคำนวณความคิดระยะทางและองศาเรขาคณิมูลฐานในปริภูมิ (หรือปริภูมิ-เวลา) โค้ง

ผิวทรงกลมคล้ายผิวโลกให้ตัวอย่างอย่างง่าย ตำแหน่ง ณ จุดใด ๆ บนผิวสามารถอธิบายได้ด้วยสองพิกัด คือ ละติจูดและลองติจูดภูมิศาสตร์ ต่างจากพิกัดคาร์ทีเชียนของระนาบ ผลต่างของพิกัดไม่เท่ากับระยะทางบนผิว ดังที่แสดงในแผนภาพด้านขวามือ สำหรับผู้ที่อยู่ ณ เส้นศูนย์สูตร การเคลื่อนไปทางตะวันตก 30 องศาลองติจูด (เส้นสีม่วงแดง) สมนัยกับระยะทางประมาณ 3,300 กิโลเมตร อีกด้านหนึ่ง ผู้ที่อยู่ละติจูด 55 องศา การเคลื่อนไปทางตะวันตก 30 องศาลองติจูด (เส้นสีน้ำเงิน) กินระยะทางเพียง 1,900 กิโลเมตร ฉะนั้นพิกัดจึงไม่ให้สารสนเทศเพียงพออธิบายเรขาคณิตของผิวทรงกลม หรือเรขาคณิตของปริภูมิหรือปริภูมิ-เวลาใด ๆ ที่ซับซ้อนกว่านั้น สารสนเทศนั้นคือสิ่งที่เข้ารหัสในเมตริกอย่างแน่นอน ซึ่งเป็นฟังก์ชันที่นิยาม ณ แต่ละจุดของผิว (หรือปริภูมิ หรือปริภูมิ-เวลา) และสัมพันธ์ผลต่างของพิกัดกับผลต่างของระยะทาง ปริมาณอื่นใดซึ่งให้ความสนใจในเรขาคณิต เช่น ความยาวของความโค้งใด ๆ หรือองศาที่เส้นโค้งสองเส้นตัดกัน สามารถคำนวณได้จากฟังก์ชันเมตริกนี้^[22]

ฟังก์ชันเมตริกและอัตราการเปลี่ยนจากจุดหนึ่งไปอีกจุดหนึ่งสามารถใช้นิยามปริมาณทางเรขาคณิตได้ เรียก เทนเซอร์ความโค้งรีมันน์ ซึ่งอธิบายว่าปริภูมิหรือปริภูมิ-เวลาโค้งอย่างไรแม่นตรงที่แต่ละจุด ในสัมพัทธภาพทั่วไป เมตริกและเทนเซอร์ความโค้งรีมันน์เป็นปริมาณที่นิยามที่แต่ละจุดในปริภูมิ-เวลา ดังที่ได้กล่าวไปแล้ว ปริมาณสสารของปริภูมิ-เวลานิยามอีกปริมาณหนึ่ง เทนเซอร์พลังงาน–โมเมนตัม T และหลักการที่ว่า "ปริภูมิ-เวลาบอกวิธีเคลื่อนที่แก่สสาร และสสารบอกวิธีโค้งแก่ปริภูมิ-เวลา" หมายความว่า ปริมาณเหล่านี้ต้องสัมพันธ์กัน ไอน์สไตน์สร้างสูตรความสัมพันธ์นี้โดยใช้เทนเซอร์ความโค้งรีมันน์และเมตริกเพื่อนิยามปริมาณทางเรขาคณิตอีกปริมาณหนึ่ง G ซึ่งบัดนี้เรียก เทนเซอร์ไอน์สไตน์ ซึ่งอธิบายวิธีโค้งของปริภูมิ-เวลาบางลักษณะ สมการของไอน์สไตน์ระบุว่า

${\displaystyle \mathbf {G} ={\frac {8\pi G}{c^{4}}}\mathbf {T} }$

กล่าวคือ ในพหุคูณค่าคงตัวหนึ่ง ปริมาณ G (ซึ่งวัดความโค้ง) เข้าสมการกับปริมาณ T (ซึ่งวัดปริมาณสสาร) ในที่นี้ G คือ ค่าคงตัวความโน้มถ่วงของความโน้มถ่วงนิวตัน และ c เป็นความเร็วแสงจากสัมพัทธภาพพิเศษ

สมการนี้มักเรียกเป็นพหูพจน์ว่า สมการของไอน์สไตน์ เนื่องจากปริมาณ G และ T ต่างกำหนดจากหลายฟังก์ชันของพิกัดปริภูมิ-เวลา และสมการต่าง ๆ เข้าสมการกับฟังก์ชันส่วนประกอบเหล่านี้^[23] ผลเฉลยของสมการเหล่านี้อธิบายเรขาคณิตเฉพาะของปริภูมิ-เวลา ตัวอย่างเช่น ผลเฉลยชวาร์ซชิลด์ (Schwarzschild solution) อธิบายเรขาคณิตรอบ ๆ มวลทรงกลมไม่หมุน เช่น ดาวฤกษ์หรือหลุมดำ ขณะที่ผลเฉลยเคอร์อธิบายหมุนดำที่หมุน กระนั้น ผลเฉลยอื่นสามารถอธิบายคลื่นความโน้มถ่วงหรือเอกภพที่กำลังขยายในกรณีของผลเฉลยฟรีดมันน์–เลแม็ทร์–โรเบิร์ตสัน–วอล์กเกอร์ ผลเฉลยง่ายที่สุด คือ ปริภูมิ-เวลามิงค็อฟสกีไม่โค้ง คือ ปริภูมิ-เวลาที่อธิบายด้วยสัมพัทธภาพพิเศษ^[24]

ไม่มีทฤษฎีวิทยาศาสตร์ใดเป็นจริงโดยโต้แย้งไม่ได้ ทฤษฎีแต่ละอย่างเป็นแบบจำลองซึ่งจำเป็นต้องตรวจสอบด้วยการทดลอง กฎความโน้มถ่วงของนิวตันเป็นที่ยอมรับเพราะคิดคำนวณการเคลื่อนที่ของดาวเคราะห์และดวงจันทร์ในระบบสุริยะโดยมีความแม่นยำพอสมควร เมื่อความแม่นยำของการวัดเชิงทดลองค่อย ๆ พัฒนาดีขึ้น จึงเริ่มมีการสังเกตข้อแตกต่างในการพยากรณ์ของนิวตันบ้าง และข้อแตกต่างเหล่านี้สามารถอธิบายได้ด้วยทฤษฎีสัมพัทธภาพทั่วไป ในทำนองเดียวกัน การพยากรณ์ของทฤษฎีสัมพัทธภาพทั่วไปจะต้องมีการตรวจสอบด้วยการทดลองด้วย และไอน์สไตน์เองประดิษฐ์การทดลองสามอย่างซึ่งปัจจุบันเรียกการทดสอบทฤษฎีคลาสสิก ดังนี้

• ความโน้มถ่วงของนิวตันพยากรณ์ว่าวงโคจรซึ่งดาวเคราะห์เดี่ยว ๆ ที่วนรอบดาวฤกษ์ทรงกลมพอดีควรเป็นวงรี ทฤษฎีของไอน์สไตน์พยากรณ์เส้นโค้งที่ซับซ้อนกว่านั้น คือ ดาวเคราะห์ประพฤติเสมือนว่ากำลังเดินทางอยู่รอบวงรีวงหนึ่ง แต่ในขณะเดียวกันวงรีทั้งวงกำลังหมุนช้า ๆ รอบดาวฤกษ์ด้วย ในแผนภาพทางขวามือ วงรีที่พยากรณ์โดยความโน้มถ่วงแบบนิวตันแสดงด้วยสีแดง และวงโคจรบางส่วนที่ไอน์สไตน์พยากรณ์แสดงด้วยสีน้ำเงิน สำหรับดาวเคราะห์ที่โคจรรอบดวงอาทิตย์ การเบี่ยงเบนจากวงโคจรของนิวตันเรียก การเลื่อนจุดใกล้ดวงอาทิตย์มากที่สุดผิดธรรมดา (anomalous perihelion shift) การวัดผลนี้ครั้งแรก สำหรับดาวพุธ ย้อนไปถึงปี 1859 ผลลัพธ์ที่แม่นยำที่สุดสำหรับดาวพุธและดาวเคราะห์อื่นจนถึงปัจจุบันอาศัยการวัดซึ่งมีการดำเนินการระหว่างปี 1966 ถึง 1990 โดยใช้กล้องโทรทรรศน์วิทยุ^[25] ทฤษฎีสัมพัทธภาพทั่วไปทำนายการเลื่อนจุดใกล้ดวงอาทิตย์มากที่สุดผิดธรรมดาสำหรับดาวเคราะห์ทุกดวงซึ่งสามารถวัดค่าดังกล่าวได้อย่างแม่นยำ (ได้แก่ ดาวพุธ ดาวศุกร์และโลก)
• สัมพันธภาพทั่วไประบุว่า แสงไม่เดินทางเป็นเส้นตรงเมื่อแผ่ในสนามความโน้มถ่วง แต่แสงกลับมีการเบนเมื่อมีเทห์ขนาดมหึมา โดยเฉพาะอย่างยิ่ง แสงดาวมีการเบนเมื่อเฉียดดวงอาทิตย์ ทำให้ตำแหน่งของดาวฤกษ์ดูเหมือนเลื่อนขึ้น 1.75 ฟิลิปดาหรืออาร์กวินาที (1 ฟิลิปดาเท่ากับ 1/3600 ขององศา) ในกรอบของความโน้มถ่วงแบบนิวตัน สามารถให้เหตุผลแบบวิทยาการศึกษาสำนึกซึ่งนำไปสู่การเบนแสงโดยกึ่งหนึ่งของปริมาณตามสัมพัทธภาพทั่วไป การพยากรณ์ที่ต่างกันสามารถทดสอบได้โดยสังเกตดาวฤกษ์ที่อยู่ใกล้ดวงอาทิตย์ระหว่างสุริยุปราคา ด้วยวิธีนี้ คณะสำรวจแอฟริกาตะวันตกของบริเตนในปี 1919 ที่มีอาเธอร์ เอ็ดดิงตันเป็นผู้นำ ยืนยันว่าการพยากรณ์ของไอน์สไตน์ถูกต้อง และการพยากรณ์ของนิวตันผิด โดยการสังเกตสุริยุปราคาเดือนพฤษภาคม 1919 ผลลัพธ์ของเอ็ดดิงตันนั้นไม่ได้แม่นยำมากนัก การสังเกตการเบนแสงของเควซาร์ที่ห่างไกลจากดวงอาทิตย์ในเวลาต่อมา ซึ่งใช้เทคนิคดาราศาสตร์วิทยุที่มีความแม่นยำสูง ยืนยันว่าผลลัพธ์ของเอ็ดดิงตันมีความแม่นยำดีกว่าอย่างสำคัญ (การวัดดังกล่าวครั้งแรกมีตั้งแต่ปี 1967 ส่วนการวิเคราะห์อย่างครอบคลุมล่าสุดมาจากปี 2004)^[26]
• ปอนด์และเร็บกาเป็นผู้สังเกตการเลื่อนไปทางแดงของความโน้มถ่วงในห้องปฏิบัติการครั้งแรกในปี 1959 นอกจากนี้ยังพบในการวัดทางฟิสิกส์ดาราศาสตร์ ซึ่งมีครั้งเด่น ๆ จากแสงที่หลบออกจากดาวแคระขาวซิริอุสบี ผลการขยายขนาดของเวลาจากความโน้มถ่วงที่สัมพันธ์กันนั้นวัดได้จากนาฬิกาอะตอมที่กำลังเคลื่อนย้ายไปที่ความสูงระหว่างหลายสิบถึงหลายหมื่นกิโลเมตร (โดยเฮเฟเลและคีตลิงในปี 1971 การวัดที่แม่นยำที่สุดในปัจจุบันวัดโดยกราวิตีโพรบ เอ ที่ปล่อยในปี 1976)^[27]

ในบรรดาการทดสอบเหล่านี้ มีเพียงการเคลื่อนที่ใกล้ดวงอาทิตย์มากที่สุดของดาวพุธเท่านั้นที่ทราบกันก่อนการเผยแพร่ครั้งสุดท้ายซึ่งสัมพัทธภาพทั่วไปของไอน์สไตน์ในปี 1916 การยืนยันการพยากรณ์ของเขาด้วยการทดลองภายหลัง โดยเฉพาะอย่างยิ่งการวันการเบนของแสงจากดวงอาทิตย์ครั้งแรกในปี 1919 ทำให้ไอน์สไตน์ได้รับชื่อเสียงในระดับนานาชาติ^[28] การทดลองทั้งสามนี้ทำให้การยอมรับสัมพัทธภาพทั่วไปเหนือกว่าทฤษฎีของนิวตันชอบด้วยเหตุผล และทางเลือกของสัมพัทธภาพทั่วไปอีกหลายทฤษฎีที่มีการเสนอไปพร้อมกัน

การทดสอบสัมพัทธภาพทั่วไปเพิ่มเติมยังได้แก่ การวัดอย่างแม่นยำซึ่งผลชาปีโรหรือการหน่วงเวลาจากความโน้มถ่วงสำหรับแสง ซึ่งมีการวัดล่าสุดในปี 2002 โดยยานอวกาศกัสซีนี–เฮยเคินส์ ชุดการทดสอบหนึ่งมุ่งเน้นผลที่ทำนายจากสัมพัทธภาพทั่วไปสำหรับพฤติกรรมของไจโรสโคปที่เคลื่อนที่ผ่านอวกาศ ผลเหล่านี้ผลหนึ่ง จีออเดสิกพรีเซสชัน (geodetic precession) มีการทดสอบด้วยการทดลองพิสัยเลเซอร์ดวงจันทร์ หรือการวัดวงโคจรของดวงจันทร์ที่มีความแม่นยำสูง การทดสอบอีกอย่างหนึ่งซึ่งเกี่ยวข้องกับมวลที่กำลังโคจร เรียก เฟรมแดรกกิง (frame-dragging) ผลจีออเดสิกและเฟรมแดรกกิงมีการทดสอบแล้วด้วยการทดลองดาวเทียมกราวิตีโพรบบีซึ่งปล่อยในปี 2004 โดยผลลัพธ์ยืนยันว่าสัมพัทธภาพมีความแม่นยำอยู่ภายใน 0.5% ถึง 15% ตามลำดับ ในเดือนธันวาคม 2008^[29]

ด้วยมาตรฐานจักรวาล ความโน้มถ่วงตลอดระบบสุริยะมีอ่อน เนื่องจากผลต่างระหว่างการพยากรณ์ของทฤษฎีไอน์สไตน์และนิวตันจะเห็นผลมากที่สุดเมื่อความโน้มถ่วงเข้ม นักฟิสิกส์จึงมีความสนใจมานานในการทดสอบผลของสัมพัทธภาพต่าง ๆ ในสภาพแวดล้อมที่มีสนามความโน้มถ่วงเข้มโดยเปรียบเทียบ จนเป็นไปได้ด้วยการสังเกตพัลซาร์คู่อย่างแม่นยำ ในระบบดาวฤกษ์ดังกล่าว ดาวนิวตรอนที่อัดแน่นอย่างสูงสองดวงโตจรรอบกันและกัน มีอย่างน้อยดวงหนึ่งเป็นพัลซาร์ วัตถุทางดาราศาสตร์ที่ปล่อยลำคลื่นวิทยุอย่างแน่น ลำคลื่นดังกล่าวมาถึงโลกด้วยระยะห่างสม่ำเสมอมาก คล้ายกับที่ลำแสงประภาคารที่หมุนอยู่หมายความว่าผู้สังเกตจะเห็นประภาคารกระพริบ และสามารถสังเกตได้ประหนึ่งชุดพัลส์ที่มีความสม่ำเสมอสูง สัมพัทธภาพทั่วไปทำนายความผันแปรที่จำเพาะจากความสม่ำเสมอของพัลส์วิทยุนี้ ตัวอย่างเช่น บางครั้งเมื่อคลื่นวิทยุผ่านเข้าใกล้ดาวนิวตรอนอีกดวงหนึ่ง คลื่นควรเบนไปด้วยผลของสนามความโน้มถ่วงดาวฤกษ์ รูปแบบพัลส์ที่สังเกตได้นั้นมีความใกล้เคียงกับที่สัมพัทธภาพทั่วไปทำนายไว้อย่างน่าประทับใจ^[30]

ชุดการสังเกตจำเพาะหนึ่งมีความสัมพันธ์กับการประยุกต์เชิงปฏิบัติที่เป็นประโยชน์อย่างเห็นได้ชัด กล่าวคือ ระบบนำทางด้วยดาวเทียมอย่างระบบกำหนดตำแหน่งบนโลกซึ่งใช้ทั้งการระบุตำแหน่งอย่างแม่นยำและการจับเวลา ระบบดังกล่าวอาศัยนาฬิกาอะตอมสองชุด คือ นาฬิกาที่อยู่บนดาวเทียมที่โคจรรอบโลก และนาฬิกาอ้างอิงที่ตั้งอยู่บนผิวโลก สัมพัทธภาพทั่วไปพยากรณ์ว่านาฬิกาสองชุดนี้ควรเดินด้วยอัตราต่างกันเล็กน้อย เนื่องจากการเคลื่อนที่ที่ต่างกัน (อันเป็นผลที่พยากรณ์ไว้ตามสัมพัทธภาพพิเศษแล้ว) และตำแหน่งที่ต่างกันในสนามความโน้มถ่วงของโลก เพื่อรับประกันความแม่นยำของระบบ นาฬิกาบนดาวเทียมจะช้าลงด้วยปัจจัยสัมพัทธภาพ หรือมีการทำให้ปัจจัยนั้นเป็นส่วนหนึ่งของอัลกอริทึมการประเมิน ฉะนั้น การทดสอบความแม่นยำของระบบ (โดยเฉพาะอย่างยิ่งการวัดอย่างถี่ถ้วนมากซึ่งเป็นส่วนหนึ่งของบทนิยามเวลาสากลเชิงพิกัด) เป็นข้อพิสูจน์ชัดเจนของความสมเหตุสมผลของการพยากรณ์สัมพัทธภาพ^[31]

มีการทดสอบอย่างอื่นจำนวนหนึ่งที่พิสูจน์ความถูกต้องของหลักกาารสมมูลฉบับต่าง ๆ สำหรับการกล่าวอย่างเข้มงวด การวัดการขยายขนาดของเวลาจากความโน้มถ่วงทั้งหมดเป็นการทดสอบฉบับอ่อนของหลักการนั้น ไม่ใช่การทดสอบสัมพัทธภาพทั่วไป จนถึงปัจจุบัน สัมพัทธภาพทั่วไปผ่านการทดสอบเชิงสังเกตทั้งหมด^[32]

แบบจำลองที่ยึดสัมพัทธภาพทั่วไปมีบทบาทสำคัญในวิชาฟิสิกส์ดาราศาสตร์ ความสำเร็จของแบบจำลองเหล่านี้ยิ่งเป็นหลักฐานความถูกต้องของทฤษฎี

ด้วยแสงมีการเบนในสนามความโน้มถ่วง จึงเป็นไปได้ที่แสงของวัตถุที่ห่างไกลมาถึงผู้สังเกตในวิถีตั้งแต่สองวิถีขึ้นไป ตัวอ่ยางเช่น แสงของวัตถุที่อยู่ห่างไกลมากอย่างควาซาร์สามารถผ่านตาด้านหนึ่งของดาราจักรขนาดมหึมาและมีการเลี้ยวเบนเล็กน้อยเพื่อมาถึงผู้สังเกตบนโลก ขณะที่แสงผ่านด้านตรงข้ามของดาราจักรเดียวกันนั้นก็มีการเลี้ยวเบนเช่นกนั จึงมาถึงผู้สังเกตเดียวกันจากทิศทางต่างไปเล็กน้อย ผลคือ ผู้สังเกตคนนั้นจะเห็นวัตถุดาราศาสตร์หนึ่งในจุดสองจุดบนท้องฟ้า โฟกัสชนิดนี้ทราบกันดีว่าพบในเลนส์ตา ฉะนั้นผลจากความโน้มถ่วงนี้จึงเรียก เลนส์ความโน้มถ่วง^[33]

ดาราศาสตร์เชิงสังเกตการณ์ใช้ผลของเลนส์เป็นเครื่องมือสำคัญในการอนุมานคุณสมบัติของวัตถุเลนส์ แม้ในกรณีที่วัตถุนั้นไม่สามารถเห็นได้โดยตรง รูปทรงของภาพจากเลนส์ให้สารสนเทศเกี่ยวกับการกระจายมวลที่เป็นสาเหตุของการเบนแสง โดยเฉพาะอย่างยิ่ง เลนส์ความโน้มถ่วงเป็นทางหนึ่งในการวัดการกระจายของสสารมืด ซึ่งไม่มีแสงแต่สามารถสังเกตได้เฉพาะจากผลความโน้มถ่วงของมัน การประยุกต์ที่น่าสนใจเป็นพิเศษได้แก่การสังเกตขนาดใหญ่ ที่ที่มวลจากเลนส์แผ่ออกเป็นบริเวณกว้างสำคัญในเอกภพที่สังเกตได้ และสามารถใช้ให้ได้มาซึ่งสารสนเทศเกี่ยวกับคุณสมบัติขนาดใหญ่และวิวัฒนาการของจักรวาลนี้^[34]

คลื่นความโน้มถ่วง (gravitational wave) ซึ่งเป็นผลสืบเนื่องโดยตรงอย่างหนึ่งของทฤษฎีของไอน์สไตน์ เป็นการบิดเบี้ยวของเรขาคณิตที่ส่งผ่านด้วยความเร็วแสง และสามารถคิดเสมือนเป็นริ้วคลื่นในปริภูมิ-เวลาได้ ทั้งนี้ ไม่ควรสับสนกับคลื่นโน้มถ่วง (gravity wave) ของพลศาสตร์ของไหล ซึ่งเป็นมโนทัศน์อีกเรื่องหนึ่ง

ในเดือนกุมภาพันธ์ 2016 ทีมแอดแวนซ์ไลโกประกาศว่าสังเกตคลื่นคนวามโน้มถ่วงโดยตรงจากการรวมหลุมดำได้^[35]

สำหรับการสังเกตโดยอ้อม ผลของคลื่นความโน้มถ่วงพบได้ในการสังเกตระบบดาวฤกษ์คู่บางระบบ ดาวฤกษ์คู่ดังกล่าวโคจรรอบกัน และขณะที่โคจรรอบกันนั้นก็ค่อย ๆ เสียพลังงานโดยแผ่คลื่นความโน้มถ่วงออกมา สำหรับดาวฤกษ์ธรรมดาอย่างดวงอาทิตย์ การเสียพลังงานนี้จะเล็กน้อยเกินไปจนตรวจไม่พบ แต่การเสียพลังงานนี้สังเกตได้ในปี 1974 ในพัลซาร์คู่ชื่อ PSR1913+16 ในระบบดังกล่าว ดาวฤกษ์ที่โคจรรอบกันดวงหนึ่งเป็นพัลซาร์ จึงมีผลลัพธ์สองประการ คือ หนึ่ง พัลซาร์เป็นวัตถุหนาแน่นยิ่งยวดที่เรียก ดาวนิวตรอน ที่การปล่อยคลื่นความโน้มถ่วงมีความเข้มกว่าดาวฤกษ์ธรรมดา และสอง พัลซาร์แผ่ลำรังสีแม่เหล็กไฟฟ้าแคบ ๆ จากขั้วแม่เหล็กของมัน เมื่อพัลซาร์หมุน ลำรังสีจะกวาดผ่านโลก ซึ่งจะเห็นลำดังกล่าวเป็นชุดพัลส์วิทยุสม่ำเสมอดุจเรือในทะเลเห็นแสงกะพริบสม่ำเสมอจากแสงที่หมุนในประภาคาร รูปแบบพัลส์วิทยุที่สม่ำเสมอนี้ทำหน้าที่เสมือนเป็น "นาฬิกา" ที่แม่นยำสูง สามารถใช้กะเวลาคาบการโคจรของดาวฤกษ์คู่ได้ และมีการตอบสนองอย่างไวต่อการบิดเบี้ยวของปริภูมิ-เวลาในละแวกติดกับมัน

ผู้ค้นพบ PSR1913+16 รัสเซล ฮัลส์และโจเซฟ เทย์เลอร์ได้รับรางวัลโนเบลสาขาฟิสิกส์ในปี 1993 นับแต่นั้น มีการค้นพบพัลซาร์คู่อื่นอีกหลายระบบ การค้นพบที่มีประโยชน์สูงสุดได้แก่ระบบที่ดาวทั้งสองดวงเป็นพัลซาร์ เพราะจะให้การทดสอบที่แม่นยำของสัมพัทธภาพทั่วไป^[36]

ปัจจุบันมีเครื่องตรวจจับคลื่นความโน้มถ่วงบนพื้นดินจำนวนหนึ่งดำเนินการอยู่ และภารกิจปล่อยเครื่องตรวจจับบนอวกาศ ไลซา (LISA) กำลังอยู่ระหว่างการพัฒนา โดยมีภารกิจก่อนหน้า (ไลซาพาธไฟน์เดอร์) ซึ่งมีการปล่อยในปี 2015 การสังเกตคลื่นความโน้มถ่วงสามารถใช้เพื่อให้ได้สารสนเทศเกี่ยวกับวัตถุเนื้อแน่นอย่างดาวนิวตรอนและหลุมดำได้ และยังใช้เพื่อสอบหาสภาพของเอกภพช่วงแรกเศษเสี้ยววินาทีหลังบิกแบง^[37]

สัมพัทธภาพทั่วไปพยากรณ์ว่าเมื่อมวลกระจุกอยู่ในบริเวณปริภูมิที่มีเนื้อแน่นเพียงพอจะเกิดหลุมดำ หลุมดำเป็นบริเวณของปริภูมิที่ผลความโน้มถ่วงเข้มเสียจนแสงก็หนีออกมาไม่ได้ คิดกันว่าหลุมดำบางชนิดเป็นขั้นสุดท้ายในวิวัฒนาการของดาวฤกษ์ขนาดมหึมา อีกด้านหนึ่ง มีการสันนิษฐานว่าหลุมดำมวลยวดยิ่งที่มีมวลหลายล้านถึงหลายพันล้านเท่าของดวงอาทิตย์อยู่ในใจกลางของดาราจักรส่วนใหญ่ และมีบทบาทสำคัญในแบบจำลองปัจจุบันวิธีการก่อกำเนิดดาราจักรในช่วงหลายพันล้านปีที่ผ่านมา^[38]

สสารที่ตกลงสู่วัตถุเนื้อแน่นเป็นกลไกที่มีประสิทธิภาพที่สุดกลไกหนึ่งสำหรับการปลดปล่อยพลังงานในรูปการแผ่รังสี และสสารที่ตกลงสู่หลุมดำเชื่อว่าเป็นตัวการให้เกิดปรากฏการณ์ทางดาราศาสตร์ที่สว่างที่สุดปรากฏการณ์หนึ่งเท่าที่จินตนาการได้ ตัวอย่างสิ่งที่น่าสนใจอย่างยิ่งโดดเด่นสำหรับนักดาราศาสตร์ได้แก่ควาซาร์และนิวเคลียสดาราจักรกัมมันต์ชนิดอื่น ภายใต้ภาวะที่ถูกต้อง สสารที่ตกลงสะสมอยู่รอบหลุมดำสามารถนำไปสู่การก่อกำเนิดเจ็ต (jet) ซึ่งเป็นลำสสารรวมปลิวออกสู่อวกาศด้วยความเร็วเกือบเท่าความเร็วแสง^[39]

มีคุณสมบัติหลายประการที่ทำให้หลุมดำเป็นบ่อเกิดของคลื่นความโน้มถ่วงที่มีโอกาสเป็นไปได้มากที่สุด เหตุผลหนึ่งคือหลุมดำเป็นวัตถุเนื้อแน่นที่สุดที่สามารถโคจรรอบกันและกันเป็นส่วนหนึ่งของระบบดาวคู่ได้ ผลคือ คลื่นความโน้มถ่วงที่ปลดปล่อยออกมาจากระบบดังกล่าวจะเข้มเป็นพิเศษ อีกเหตุผลหนึ่งสืบเนื่องจากสิ่งที่เรียกว่าทฤษฎีบทความเป็นได้อย่างเดียวของหลุมดำ คือเมื่อเวลาผ่านไปหลุมดำจะยังมีเฉพาะคุณลักษณะแตกต่างน้อยที่สุด (ทฤษฎีบทเหล่านี้ได้ชื่อว่า ทฤษฎี "ไร้ขน") โดยไม่ขึ้นอยู่กับรูปทรงเรขาคณิตตั้งต้น ตัวอย่างเช่น ในระยะยาว การยุบตัวของลูกบาศก์สสารในทางทฤษฎีจะไม่ส่งผลให้เกิดหลุมดำทรงลูกบาศก์ แต่หลุมดำที่เกิดขึ้นจากไม่แตกต่างกับหลุมดำที่เกิดจากการยุบตัวของมวลทรงกลม ในการเปลี่ยนผ่านรูปทรงกลม หลุมดำที่เกิดจากการยุบตัวของรูปทรงที่ซับซ้อนมากขึ้นจะปลดปล่อยคลื่นความโน้มถ่วง^[40]

ลักษณะสำคัญที่สุดอย่างหนึ่งของสัมพัทธภาพทั่วไปคือสามารถใช้ได้กับเอกภพทั้งหมด จุดสำคัญคือในมาตราส่วนใหญ่ เอกภพนี้ดูเหมือนสร้างอยู่บนเส้นตรงเรียบง่ายมาก ๆ คือ ทุกการสังเกตในปัจจุบันเสนอว่าโดยเฉลี่ยโครงสร้างของจักรวาลควรคงเดิมโดยประมาณ โดยไม่ขึ้นอยู่กับสถานที่ของผู้สังเกตหรือทิศทางของการสังเกต เอกภพเป็นเนื้อเดียวกันและไอโซทรอปี (ภาวะเอกรูป) โดยประมาณ เอกภพที่ง่ายโดยเปรียบเทียบนี้สามารถอธิบายได้ด้วยผลเฉลยง่ายของสมการของไอน์สไตน์ แบบจำลองจักรวาลวิทยาของเอกภพปัจจุบันได้มาจากการรวมผลเฉลยง่าย ๆ เหล่านี้กับสัมพัทธภาพทั่วไปโดยทฤษฎีที่อธิบายคุณสมบัติของปริมาณสสารของเอกภพ ได้แก่ อุณหพลศาสตร์ ฟิสิกส์นิวเคลียร์และฟิสิกส์อนุภาค ตามแบบจำลองเหล่านี้ เอกภพปัจจุบันแห่งนี้ถือกำเนิดจากภาวะอุณหภูมิสูงและหนาแน่นยิ่งยวด ที่เรียก บิกแบง ทีเมื่อประมาณ 14,000 ล้านปีก่อนและมีการขยายตัวนับแต่นั้น^[41]

สมการของไอน์สไตน์สามารถวางนัยทั่วไปได้โดยการเพิ่มพจน์ที่เรียก ค่าคงที่จักรวาลวิทยา เมื่อมีพจน์นี้อยู่ ปริภูมิว่างเองจะประพฤติตนเป็นแหล่งความโน้มถ่วงดึงดูด (หรือที่พบน้อยกว่า ผลัก) ไอน์สไตน์นำเสนอพจน์นี้ครั้งแรกในเอกสารบุกเบิกปี 1917 ว่าด้วยจักรวาลวิทยา โดยมีแรงจูงใจจำเพาะมาก คือ ความคิดจักรวาลวิทยาร่วมสมัยถือว่าเอกภาพเป็นสถิต และต้องอาศัยอีกพจน์หนึ่งเพื่อสร้างเอกภพแบบจำลองสถิติภายในกรอบของสัมพัทธภาพทั่วไป เมื่อชัดเจนว่าเอกภพไม่ใช่สถิต แต่กำลังขยายตัว ไอน์สไตน์จึงรีบทิ้งพจน์ใหม่นี้ นับแต่สิ้นสุดคริสต์ทศวรรษ 1990 อย่างไรก็ตาม หลักฐานดาราศาสตร์บ่งชี้ว่าการขยายตัวที่มีความเร่งนี้ต้องกันกับค่าคงที่จักรวาลวิทยา หรือเทียบเท่ากับพลังงานมืดชนิดที่จำเพาะและพบทั่วไป กำลังสะสมอย่างคงที่^[42]

สัมพัทธภาพทั่วไปประสบความสำเร็จอย่างมากในการให้กรอบสำหรับแบบจำลองที่แม่นยำซึ่งอธิบายกลุ่มปรากฏการณ์ทางฟิสิกส์หลายอย่างน่าประทับใจ อีกด้านหนึ่ง ยังมีคำถามที่ยังไม่มีคำถามที่น่าสนใจหลายข้อ และโดยเฉพาะอย่างยิ่ง ตัวทฤษฎีโดยรวมเกือบแน่นอนว่าไม่เสร็จสมบูรณ์^[43]

สัมพัทธภาพทั่วไปเป็นทฤษฎีคลาสสิก หมายความว่า ทฤษฎีนี้ไม่รวมผลของฟิสิกส์ควอนตัม ทำให้แตกต่างจากทฤษฎีอันตรกิริยาพื้นฐานสมัยใหม่อื่นทั้งหมด การแสวงสัมพัทธภาพทั่วไปฉบับควอนตัมเป็นปัญหาที่ยังต้องการคำตอบมูลฐานที่สุดคำถามหนึ่งในวิชาฟิสิกส์ แม้มีผู้ท้าชิงที่มีแววอย่างทฤษฎีความโน้มถ่วงเชิงควอนตัม โดยเฉพาะอย่างยิ่งทฤษฎีสตริงและความโน้มถ่วงเชิงควอนตัมวงวน แต่ในปัจจุบันยังไม่มีทฤษฎีที่ต้องกันและสมบูรณ์ มีผู้หวังมายาวนานว่าทฤษฎีความโน้มถ่วงเชิงควอนตัมจะกำจัดคุณลักษณะที่เป็นปัญหาอีกประการหนึ่งของสัมพัทธภาพทั่วไป ได้แก่ การมีภาวะเอกฐานของปริภูมิ-เวลา ภาวะเอกฐานเหล่านี้เป็นเขตแดน ("ขอบคม") ของปริภูมิ-เวลาซึ่ง ณ ที่นั้นเรขาคณิตจะนิยามไม่ชัดเจน โดยมีผลคือสัมพัทธภาพทั่วไปจะเสียอำนาจในการพยากรณ์ ยิ่งไปกว่านั้น ยังมีสิ่งที่เรียกทฤษฎีบทภาวะเอกฐานซึ่งพยากรณ์ว่าภาวะเอกฐานดังกล่าวจะต้องมีอยู่ในเอกภพหากจะยึดถือกฎสัมพัทธภาพทั่วไปโดยไม่มีการดัดแปรทางควอนตัมใด ๆ ตัวอย่างขึ้นชื่อที่สุด ได้แก่ ภาวะเอกฐานที่สัมพันธ์กับเอกภพจำลองซุ่งอธิบายหลุมดำและจุดเริ่มต้นของเอกภพ^[44]

มีความพยายามอื่นในการดัดแปรสัมพัทธภาพทั่วไปในบริบทจักรวาลวิทยา ในแบบจำลองจักรวาลวิทยาสมัยใหม่ พลังงานส่วนใหญ่ในเอกภพอยู่ในรูปที่ไม่เคยมีการตรวจพบโดยตรง เรียก พลังงานมืดและสสารมืด มีข้อเสนอซึ่งเป็นที่ถกเถียงกันหลายข้อเพื่อลบความจำเป็นพลังงานและสสารแบบที่อธิบายเข้าใจได้ยาก โดยการดัดแปรกฎที่ว่าด้วยความโน้มถ่วงและพลศาสตร์การขยายตัวของจักรวาล ตัวอย่างเช่น พลศาสตร์นิวตันแบบปรับปรุงใหม่^[45]

นอกจากความท้าทายของผลควอนตัมและจักรวาลวิทยาแล้ว การวิจัยเรื่องสัมพัทธภาพทั่วไปยังเต็มไปด้วยโอกาสสำหรับการสำรวจต่อไป นักสัมพัทธภาพทางคณิตศาสตร์สำรวจสภาพของภาวะเอกฐานและคุณสมบัติมูลฐานของสมการของไอน์สไตน์ และการจำลองคอมพิวเตอร์ที่ครอบคลุมมากขึ้นกว่าแต่ก่อนของปริภูมิ-เวลาจำเพาะ (เช่น ปริภูมิ-เวลาที่อธิบายหลุมดำที่กำลังรวมตัวกัน) ก็มีการดำเนินงานแล้ว^[46] ตั้งแต่กว่าเก้าสิบปีหลังมีการเผยแพร่ทฤษฎีนี้ครั้งแรก การวิจัยยิ่งมีความเคลื่อนไหวมากว่าที่เคย^[47]

• Ashby, Neil (2002), "Relativity and the Global Positioning System" (PDF), Physics Today, 55 (5): 41–47, Bibcode:2002PhT....55e..41A, doi:10.1063/1.1485583
• Ashby, Neil (2003), "Relativity in the Global Positioning System", Living Reviews in Relativity, 6: 1, Bibcode:2003LRR.....6....1A, doi:10.12942/lrr-2003-1, คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2007-07-04, สืบค้นเมื่อ 2007-07-06
• Bartusiak, Marcia (2000), Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time, Berkley, ISBN 978-0-425-18620-6
• Berry, Michael V. (1989), Principles of Cosmology and Gravitation (2nd ed.), Institute of Physics Publishing, ISBN 0-85274-037-9
• Bertotti, Bruno (2005), "The Cassini Experiment: Investigating the Nature of Gravity", ใน Renn, Jürgen (บ.ก.), One hundred authors for Einstein, Wiley-VCH, pp. 402–405, ISBN 3-527-40574-7
• Blair, David; McNamara, Geoff (1997), Ripples on a Cosmic Sea. The Search for Gravitational Waves, Perseus, ISBN 0-7382-0137-5
• Caldwell, Robert R. (2004), "Dark Energy", Physics World, 17: 37–42, doi:10.1088/2058-7058/17/5/36
• Chrusciel, Piotr (2006), "How many different kinds of black hole are there?", Einstein Online, คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2011-04-14, สืบค้นเมื่อ 2007-07-15
• Cowen, Ron (2001), "A Dark Force in the Universe", Science News, Society for Science &#38, 159 (14): 218, doi:10.2307/3981642, JSTOR 3981642
• Disney, Michael (1998), "A New Look at Quasars", Scientific American, 278 (6): 52–57, Bibcode:1998SciAm.278f..52D, doi:10.1038/scientificamerican0698-52
• Ehlers, Jürgen; Rindler, Wolfgang (1997), "Local and Global Light Bending in Einstein's and other Gravitational Theories", General Relativity and Gravitation, 29 (4): 519–529, Bibcode:1997GReGr..29..519E, doi:10.1023/A:1018843001842
• Einstein, Albert (1917), "Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie", Sitzungsberichte der Preußischen Akademie der Wissenschaften: 142
• Einstein, Albert (1961), Relativity. The special and general theory, Crown Publishers
• Friedrich, Helmut (2005), "Is general relativity 'essentially understood'?", Annalen der Physik, 15 (1–2): 84–108, arXiv:gr-qc/0508016, Bibcode:2006AnP...518...84F, doi:10.1002/andp.200510173
• Geroch, Robert (1978), General relativity from A to B, University of Chicago Press, ISBN 0-226-28864-1
• Giulini, Domenico (2005), Special relativity. A first encounter, Oxford University Press, ISBN 0-19-856746-4
• Gnedin, Nickolay Y. (2005), "Digitizing the Universe", Nature, 435 (7042): 572–573, Bibcode:2005Natur.435..572G, doi:10.1038/435572a, PMID 15931201
• Greene, Brian (1999), The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory, Vintage, ISBN 0-375-70811-1
• Greene, Brian (2004), The Fabric of the Cosmos: Space, Time, and the Texture of Reality, A. A. Knopf, Bibcode:2004fcst.book.....G, ISBN 0-375-41288-3
• Harrison, David M. (2002), A Non-mathematical Proof of Gravitational Time Dilation (PDF), สืบค้นเมื่อ 2007-05-06
• Hartl, Gerhard (2005), "The Confirmation of the General Theory of Relativity by the British Eclipse Expedition of 1919", ใน Renn, Jürgen (บ.ก.), One hundred authors for Einstein, Wiley-VCH, pp. 182–187, ISBN 3-527-40574-7
• Hogan, Craig J. (1999), The Little Book of the Big Bang. A Cosmic Primer, Springer, ISBN 0-387-98385-6
• Janssen, Michel (2005), "Of pots and holes: Einstein's bumpy road to general relativity" (PDF), Annalen der Physik, 14 (S1): 58–85, Bibcode:2005AnP...517S..58J, doi:10.1002/andp.200410130, คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2017-07-13, สืบค้นเมื่อ 2019-04-19
• Kennefick, Daniel (2005), "Astronomers Test General Relativity: Light-bending and the Solar Redshift", ใน Renn, Jürgen (บ.ก.), One hundred authors for Einstein, Wiley-VCH, pp. 178–181, ISBN 3-527-40574-7
• Kennefick, Daniel (2007), "Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition", Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005, vol. 0709, p. 685, arXiv:0709.0685, Bibcode:2007arXiv0709.0685K
• Kramer, Michael (2004), "Millisecond Pulsars as Tools of Fundamental Physics", ใน Karshenboim, S. G.; Peik, E. (บ.ก.), Astrophysics, Clocks and Fundamental Constants (Lecture Notes in Physics Vol. 648), Springer, pp. 33–54 (E-Print at astro-ph/0405178 เก็บถาวร 2017-11-05 ที่ เวย์แบ็กแมชชีน)
• Lehner, Luis (2002), "Numerical Relativity: Status and Prospects", Proceedings of the 16th International Conference on General Relativity and Gravitation, held 15–21 July 2001 in Durban, p. 210, arXiv:gr-qc/0202055, Bibcode:2002grg..conf..210L, doi:10.1142/9789812776556_0010, ISBN 978-981-238-171-2
• Lochner, Jim, บ.ก. (2007), "Gravitational Lensing", Imagine the Universe website, NASA GSFC, คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2007-06-17, สืบค้นเมื่อ 2007-06-12
• Maddox, John (1998), What Remains To Be Discovered, Macmillan, ISBN 0-684-82292-X
• Mermin, N. David (2005), It's About Time. Understanding Einstein's Relativity, Princeton University Press, ISBN 0-691-12201-6
• Milgrom, Mordehai (2002), "Does dark matter really exist?", Scientific American, 287 (2): 30–37, Bibcode:2002SciAm.287b..42M, doi:10.1038/scientificamerican0802-42
• Norton, John D. (1985), "What was Einstein's principle of equivalence?" (PDF), Studies in History and Philosophy of Science, 16 (3): 203–246, doi:10.1016/0039-3681(85)90002-0, สืบค้นเมื่อ 2007-06-11
• Newbury, Pete (1997), Gravitational lensing webpages, คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2012-12-06, สืบค้นเมื่อ 2007-06-12
• Nieto, Michael Martin (2006), "The quest to understand the Pioneer anomaly" (PDF), EurophysicsNews, 37 (6): 30–34, arXiv:gr-qc/0702017, Bibcode:2006ENews..37...30N, doi:10.1051/epn:2006604, คลังข้อมูลเก่าเก็บจากแหล่งเดิม (PDF)เมื่อ 2007-06-29
• Pais, Abraham (1982), 'Subtle is the Lord ...' The Science and life of Albert Einstein, Oxford University Press, ISBN 0-19-853907-X
• Penrose, Roger (2004), The Road to Reality, A. A. Knopf, ISBN 0-679-45443-8
• Pössel, M. (2007), "The equivalence principle and the deflection of light", Einstein Online, คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2007-05-03, สืบค้นเมื่อ 2007-05-06
• Poisson, Eric (2004), "The Motion of Point Particles in Curved Spacetime", Living Rev. Relativ., 7, arXiv:gr-qc/0306052, Bibcode:2004LRR.....7....6P, doi:10.12942/lrr-2004-6, สืบค้นเมื่อ 2007-06-13
• Renn, Jürgen, บ.ก. (2005), Albert Einstein – Chief Engineer of the Universe: Einstein's Life and Work in Context, Berlin: Wiley-VCH, ISBN 3-527-40571-2
• Robson, Ian (1996), Active galactic nuclei, John Wiley, ISBN 0-471-95853-0
• Schutz, Bernard F. (2003), Gravity from the ground up, Cambridge University Press, ISBN 0-521-45506-5
• Smolin, Lee (2001), Three Roads to Quantum Gravity, Basic, ISBN 0-465-07835-4
• von Soldner, Johann Georg (1804), "Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht" , Berliner Astronomisches Jahrbuch: 161–172.
• Sparke, Linda S.; Gallagher, John S. (2007), Galaxies in the universe – An introduction, Cambridge University Press, ISBN 0-521-85593-4
• Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos S.; Yoshida, N; Gao, L; Navarro, J; Thacker, R; Croton, D; และคณะ (2005), "Simulations of the formation, evolution and clustering of galaxies and quasars" (PDF), Nature, 435 (7042): 629–636, arXiv:astro-ph/0504097, Bibcode:2005Natur.435..629S, doi:10.1038/nature03597, PMID 15931216
• Stachel, John (1989), "The Rigidly Rotating Disk as the 'Missing Link in the History of General Relativity'", ใน Howard, D.; Stachel, J. (บ.ก.), Einstein and the History of General Relativity (Einstein Studies, Vol. 1), Birkhäuser, pp. 48–62, ISBN 0-8176-3392-8
• Thorne, Kip (1994), Black Holes and Time Warps: Einstein's Outrageous Legacy, W W Norton & Company, ISBN 0-393-31276-3
• Trimble, Virginia; Barstow, Martin (2007), "Gravitational redshift and White Dwarf stars", Einstein Online, คลังข้อมูลเก่าเก็บจากแหล่งเดิมเมื่อ 2011-08-28, สืบค้นเมื่อ 2007-06-13
• Wheeler, John A. (1990), A Journey Into Gravity and Spacetime, Scientific American Library, San Francisco: W. H. Freeman, ISBN 0-7167-6034-7
• Will, Clifford M. (1993), Was Einstein Right?, Oxford University Press, ISBN 0-19-286170-0
• Will, Clifford M. (2006), "The Confrontation between General Relativity and Experiment", Living Rev. Relativ., 9: 3, arXiv:gr-qc/0510072, Bibcode:2006LRR.....9....3W, doi:10.12942/lrr-2006-3, สืบค้นเมื่อ 2007-06-12
• Wright, Ned (2007), Cosmology tutorial and FAQ, University of California at Los Angeles, สืบค้นเมื่อ 2007-06-12

วิกิมีเดียคอมมอนส์มีสื่อที่เกี่ยวข้องกับ บทนำทฤษฎีสัมพัทธภาพทั่วไป

• Einstein Online เก็บถาวร 2014-06-01 ที่ เวย์แบ็กแมชชีน. Website featuring articles on a variety of aspects of relativistic physics for a general audience, hosted by the Max Planck Institute for Gravitational Physics