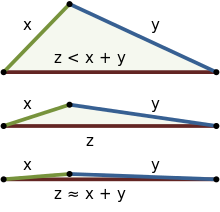
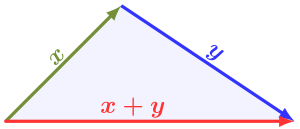
Три приклади нерівності трикутника для трикутників зі сторонами з довжинами x y z z x + y z x + y Нерівність трикутника — основна властивість геометричних фігур евклідового простору, відстані , що використовується в геометрії , функціональному аналізі .
Вона стверджує, що будь-яка сторона довільного трикутника менша за суму двох інших його сторін та більша за їх різницю.
Нерівність трикутника входить як аксіома в визначення метрики простору , норми .
Евклідова побудова доведення нерівності трикутника для планиметрії. Нерівність трикутника є теоремою в Евклідовій геометрії , доведення наведено ще в «Началах» Евкліда .
В трикутнику
Δ
A
B
C
:
|
A
C
|
⩽
|
A
B
|
+
|
B
C
|
,
{\displaystyle \ \Delta ABC:\;\;|AC|\leqslant |AB|+|BC|,}
|
A
C
|
=
|
A
B
|
+
|
B
C
|
{\displaystyle \ |AC|=|AB|+|BC|}
B
{\displaystyle B}
A
{\displaystyle A}
C
{\displaystyle C}
Нерівність трикутника для норм векторів. Якщо
(
V
,
‖
⋅
‖
)
{\displaystyle (V,\|\cdot \|)}
нормований векторний простір , де
V
{\displaystyle V}
множина , а
‖
⋅
‖
{\displaystyle \|\cdot \|}
V
{\displaystyle V}
норма . Тоді за визначенням норми :
‖
x
+
y
‖
⩽
‖
x
‖
+
‖
y
‖
,
∀
x
,
y
∈
V
.
{\displaystyle \|x+y\|\leqslant \|x\|+\|y\|,\quad \forall x,y\in V.}
Якщо
(
X
,
ρ
)
{\displaystyle \ (X,\rho )}
метричний простір , де
X
{\displaystyle X}
ρ
{\displaystyle \ \rho }
X
{\displaystyle X}
метрика . Тоді за визначенням метрики:
ρ
(
x
,
y
)
⩽
ρ
(
x
,
z
)
+
ρ
(
z
,
y
)
,
x
,
y
,
z
∈
X
.
{\displaystyle \rho (x,y)\leqslant \rho (x,z)+\rho (z,y),\quad x,y,z\in X.}
Наслідком нерівності трикутника в нормованому та метричному просторі є такі нерівності:
|
‖
x
‖
−
‖
y
‖
|
⩽
‖
x
−
y
‖
,
x
,
y
∈
V
;
{\displaystyle {\bigl |}\|x\|-\|y\|{\bigr |}\leqslant \|x-y\|,\quad x,y\in V;}
|
ρ
(
x
,
y
)
−
ρ
(
x
,
z
)
|
⩽
ρ
(
y
,
z
)
,
x
,
y
,
z
∈
X
.
{\displaystyle |\rho (x,y)-\rho (x,z)|\leqslant \rho (y,z),\quad x,y,z\in X.}
Види трикутників Чудові лінії Чудові точки Основні теореми Додаткові теореми Узагальнення Інше