生日攻擊 是密碼學 的一種破譯 手段,利用了機率論 中的生日問題 ,用於干擾兩個或以上群體之間的通訊。此攻擊是對固定的重新排列模式作隨機嘗試攻擊,仰賴較高的命中率(鴿籠原理 )。生日攻擊可在
2
n
=
2
n
/
2
{\textstyle {\sqrt {2^{n}}}=2^{n/2}}
雜湊碰撞 ,低於原像攻擊 的
2
n
{\textstyle 2^{n}}
[ 1] 量子電腦 能夠進行生日攻擊,進而可以破解防雜湊碰撞 的抵禦,並能把時間壓縮到
2
n
3
=
2
n
/
3
{\textstyle {\sqrt[{3}]{2^{n}}}=2^{n/3}}
[ 2]
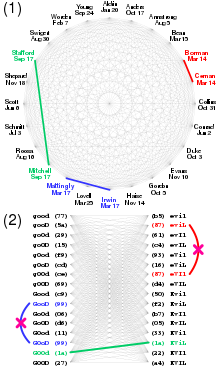
比較生日問題 (1) 和生日攻擊 (2):
在(1)中,碰撞發生在同一組內,例如:24 位登月太空人中,276 組配對中有 3 組生日相同。
在(2)中,碰撞發生在兩組之間,例如:針對良性和惡意合約各16種變體,取其SHA-256雜湊值的第一個位元組,256組配對中找到1組碰撞。 舉例來說,假設有一位老師帶著一個有30位學生(n = 30)的班級,老師詢問每位學生的生日(為了簡化計算,忽略閏年 ),想要確認是否有兩位學生的生日相同(這相當於稍後會提到的雜湊碰撞)。 直覺上,這個機率可能看起來很小。 但出乎意料的是,根據公式
1
−
365
!
(
365
−
n
)
!
⋅
365
n
{\displaystyle 1-{\frac {365!}{(365-n)!\cdot 365^{n}}}}
[ 3]
如果老師挑選了一個特定的日期(例如 9 月 16 日),那麼至少有一位學生在該特定日期出生的機率是
1
−
(
364
/
365
)
30
{\displaystyle 1-(364/365)^{30}}
在生日攻擊中,攻擊者會準備多個不同版本的良性和惡意合約,每個合約都有一個數位簽章 。 目標是尋找一對具有相同簽章的良性和惡意合約。 在這個假設的例子中,假設字串的數位簽章是其SHA-256 雜湊值的第一個位元組。 找到的組合將以綠色表示——需要注意的是,找到兩個良性合約(藍色)或兩個惡意合約(紅色)的配對是無效的的。 當受害者接受良性合約後,攻擊者會將其替換為惡意合約,並聲稱受害者已簽署該合約,因為數位簽章作為證據可以證明此。
定函数
f
{\displaystyle f}
f
(
x
1
)
=
f
(
x
2
)
{\displaystyle f(x_{1})=f(x_{2})}
x
1
,
x
2
{\displaystyle x_{1},x_{2}}
x
1
,
x
2
{\displaystyle x_{1},x_{2}}
碰撞 。找出一對碰撞的方法可以是隨機或偽隨機地輸入不同的數值,直到找出至少兩個相同的結果為止。但由於生日問題,這種方法的效率不高。明確的說,若函数
f
(
x
)
{\displaystyle f(x)}
H
{\displaystyle H}
H
{\displaystyle H}
f
(
x
1
)
=
f
(
x
2
)
{\displaystyle f(x_{1})=f(x_{2})}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
1.25
H
{\displaystyle 1.25{\sqrt {H}}}
思考下面一个实验。从下列的H 数集中随机均匀地选择n 个值,因此将允许重复。使p (n ; H )成为此实验中至少一个值被选择多于一次的概率。则概率可估计为
p
(
n
;
H
)
≈
1
−
e
−
n
(
n
−
1
)
/
(
2
H
)
≈
1
−
e
−
n
2
/
(
2
H
)
{\displaystyle p(n;H)\approx 1-e^{-n(n-1)/(2H)}\approx 1-e^{-n^{2}/(2H)}}
使n (p ; H )为将选择的最小数值,这种情况下找到碰撞的概率至少为 p 。通过颠倒上方的表达式,可得到了下列估计公式:
n
(
p
;
H
)
≈
2
H
ln
1
1
−
p
{\displaystyle n(p;H)\approx {\sqrt {2H\ln {\frac {1}{1-p}}}}}
将碰撞概率设为0.5,将得到
n
(
0.5
;
H
)
≈
1.1774
H
{\displaystyle n(0.5;H)\approx 1.1774{\sqrt {H}}}
使Q (H )成为在寻找首次碰撞前所期望的值的数量。此数量可通过下列公式进行估计:
Q
(
H
)
≈
π
2
H
{\displaystyle Q(H)\approx {\sqrt {{\frac {\pi }{2}}H}}}
举例:若使用64位哈希,则估计将有1.8 × 1019 个不同的输出。若这些输出均可能发生(理想情况下),则攻击者“仅仅”需要约50亿次尝试(5.38 × 109 )就能通过暴力攻击生成碰撞。此值被称为 生日界限 (birthday bound)[ 4] n 位密码则需要2n /2[ 5]
位数
可能输出(H)
期望的随机碰撞可能性
10−18
10−15
10−12
10−9
10−6
0.1%
1%
25%
50%
75%
16
216 (~6.5 x 104 )
<2
<2
<2
<2
<2
11
36
190
300
430
32
232 (~4.3 × 109 )
<2
<2
<2
3
93
2900
9300
50,000
77,000
110,000
64
264 (~1.8 × 1019 )
6
190
6100
190,000
6,100,000
1.9 × 108
6.1 × 108
3.3 × 109
5.1 × 109
7.2 × 109
128
2128 (~3.4 × 1038 )
2.6 × 1010
8.2 × 1011
2.6 × 1013
8.2 × 1014
2.6 × 1016
8.3 × 1017
2.6 × 1018
1.4 × 1019
2.2 × 1019
3.1 × 1019
256
2256 (~1.2 × 1077 )
4.8 × 1029
1.5 × 1031
4.8 × 1032
1.5 × 1034
4.8 × 1035
1.5 × 1037
4.8 × 1037
2.6 × 1038
4.0 × 1038
5.7 × 1038
384
2384 (~3.9 × 10115 )
8.9 × 1048
2.8 × 1050
8.9 × 1051
2.8 × 1053
8.9 × 1054
2.8 × 1056
8.9 × 1056
4.8 × 1057
7.4 × 1057
1.0 × 1058
512
2512 (~1.3 × 10154 )
1.6 × 1068
5.2 × 1069
1.6 × 1071
5.2 × 1072
1.6 × 1074
5.2 × 1075
1.6 × 1076
8.8 × 1076
1.4 × 1077
1.9 × 1077
表格展示了需要达到给定成功可能性的哈希数量n (p ),且假设所有哈希均有相同概率。为了比较,通常一块硬盘的不可修正比特错误率为10−18 至10−15 。[ 6] MD5 哈希或通用唯一识别码 将在8200亿份文档时得到破解,即使它们的可能输出还要更多。 显而易见,若函数的输出不平均分布,碰撞则可能将被更快找到。哈希函数的“平衡”概念量化了其能抵御生日攻击(攻击平均的密钥分布)的次数。然而,确定哈希函数的平衡将需要计算所有输入,因此这种方法对于诸如MD及SHA系的流行哈希函数是不切实际的。[ 7]
n
(
p
;
H
)
{\displaystyle n(p;H)}
ln
1
1
−
p
{\displaystyle \ln {\frac {1}{1-p}}}
log(1/(1-p)),公式由于有效位丢失
p
{\displaystyle p}
log1p(如C99 中一样)可用时,应直接使用可达到相同效果的表达式-log1p(-p)。[ 8]
下列是能准确生成上方表格中大多数数值的Python 函数:
from math import log1p , sqrt
def birthday ( probability_exponent , bits ):
probability = 10.0 ** probability_exponent
outputs = 2.0 ** bits
return sqrt ( 2.0 * outputs *- log1p ( - probability ))
若代码保存在命名为birthday.py的文件中,用户可和下面的例子一样交互运行此程序:
$ python -i birthday.py
>>> birthday(-15, 128)
824963474247.1193
>>> birthday(-6, 32)
92.68192319417072
一项經驗法則 可适用于此关系中的心算 流程
p
(
n
)
≈
n
2
2
H
{\displaystyle p(n)\approx {n^{2} \over 2H}}
可改写为
H
≈
n
2
2
p
(
n
)
{\displaystyle H\approx {n^{2} \over 2p(n)}}
或
n
≈
2
H
×
p
(
n
)
{\displaystyle n\approx {\sqrt {2H\times p(n)}}}
此公式在概率小于等于0.5时有效。
此近似方案在使用指数时可轻易使用。例如,假设构建32位哈希(
H
=
2
32
{\displaystyle H=2^{32}}
p
≈
2
−
20
{\displaystyle p\approx 2^{-20}}
n
≈
2
×
2
32
×
2
−
20
=
2
1
+
32
−
20
=
2
13
=
2
6.5
≈
90.5
{\displaystyle n\approx {\sqrt {2\times 2^{32}\times 2^{-20}}}={\sqrt {2^{1+32-20}}}={\sqrt {2^{13}}}=2^{6.5}\approx 90.5}
即与正确答案93次近似。
數位簽章 可对生日攻击十分敏感。设想一条被首次计算
f
(
m
)
{\displaystyle f(m)}
f
{\displaystyle f}
密碼雜湊函數 )所签名的信息,且随后又使用了一些密钥来签名
f
(
m
)
{\displaystyle f(m)}
愛麗絲與鮑伯 牵涉到签名詐騙 合同。马洛里准备了一份正常合同
m
{\displaystyle m}
m
′
{\displaystyle m'}
m
{\displaystyle m}
m
{\displaystyle m}
相似情况下,马洛里也为伪造合同
m
′
{\displaystyle m'}
f
(
m
)
=
f
(
m
′
)
{\displaystyle f(m)=f(m')}
此例中,攻击概率与原始的生日问题稍有不同,因为马洛里将在寻找两份具有相同哈希的正常合同与伪造合同时将一无所获。马洛里的策略是生成一份伪造和一份正常的合同。生日问题公式适用于
n
{\displaystyle n}
2
n
{\displaystyle 2n}
为避免这种攻击,用于签名方案的哈希函数的输出长度应够大以从计算角度防止生日攻击。换言之,位数应为防止普通暴力破解 所需位数的两倍。
除了使用更大的位数长度外,签名者(鲍勃)可以在签名前做出一些随机且无害的更改,并且在自己的手上留下一份合同副本以在法庭上展示出他的签名与正常合同上的匹配,而不匹配伪造合同。
离散对数的波拉德ρ算法 是使用生日攻击以计算离散对数 的算法。
米希尔·贝拉尔 EUROCRYPT 《应用密码学》, 第二版。(Applied Cryptography, 2nd ed.) 布魯斯·施奈爾 所著


![{\textstyle {\sqrt[{3}]{2^{n}}}=2^{n/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e4fca0369ec77e6f37ff549c6e568eab93bf3b8)




























