Teorema Pompeiu

Teorema hasil geometri bidang oleh Dimitrie Pompeiu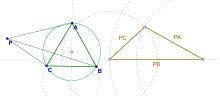

Teorema Pompeiu adalah teorema hasil dari geometri bidang, yang ditemukan oleh matematikawan Rumania Dimitrie Pompeiu.

Teorema ini dinyatakan sebagai berikut :

Diketahui segitiga sama sisi ABC pada bidang, dan titik P pada bidang segitiga ABC, panjang PA, PB, dan PC membentuk (mungkin, degenerasi) sisi segitiga ^[1][2]

Dimitrie Pompeiu menerbitkan teorema ini pada tahun 1936, akan tetapi matematikawan Jerman August Ferdinand Möbius telah menerbitkan teorema yang lebih umum tentang empat titik di bidang Euclidean pada tahun 1852. Möbius juga telah menurunkan pernyataan teorema Pompeiu secara eksplisit sebagai suatu kasus istimewa dari teoremanya yang mana lebih umum. Dengan demikian, teorema ini juga dikenal sebagai teorema Möbius-Pompeiu .^[3]

Dimisalkan sebuah rotasi 60° searah jarum jam terhadap titik B suatu segitiga sama sisi. Anggap titik A memetakan ke titik C, dan titik P memetakan ke titik P ' . Maka ${\displaystyle \scriptstyle garis\ PB\ =\ garis\ P'B}$, dan ${\displaystyle \scriptstyle \angle PBP'\ =\ 60^{\circ }}$ . Sehingga segitiga PBP ' berukuran sama sisi dan ${\displaystyle \scriptstyle garis\ PP'\ =\ garis\ PB}$ dan ${\displaystyle \scriptstyle PA\ =\ P'C}$ . Jadi, segitiga PCP ' memiliki sisi yang sama panjang dengan PA, PB, dan PC. (lihat gambar).^[1][2]

Perhitungan lebih lanjut menjelaskan jika titik P tidak terletak di bagian dalam segitiga, melainkan ada di dalam lingkaran, maka PA, PB, PC membentuk segitiga merosot, dengan sisi yang terbesar sama dengan jumlah yang lain, Hal ini juga dikenal sebagai teorema Van Schooten .^[1]

• MathWorld pada Teorema Pompeiu
• Teorema Pompeiu di cut-the-knot.org
• Teorema Pompeiu di https://kencanadewidotnet.wordpress.com/2012/02/05/teorema-pompeiu/

1. ^ ^{a b c} Jozsef Sandor: On the Geometry of Equilateral Triangles. Forum Geometricorum, Volume 5 (2005), pp. 107–117
2. ^ ^{a b} Titu Andreescu, Razvan Gelca: Mathematical Olympiad Challenges. Springer, 2008, ISBN 9780817646110, pp. 4-5 Kesalahan pengutipan: Tanda <ref> tidak sah; nama "Titu" didefinisikan berulang dengan isi berbeda
3. ^ D. MITRINOVIĆ, J. PEČARIĆ, J., V. VOLENEC: History, Variations and Generalizations of the Möbius-Neuberg theorem and the Möbius-Ponpeiu. Bulletin Mathématique De La Société Des Sciences Mathématiques De La République Socialiste De Roumanie, 31 (79), no. 1, 1987, pp. 25–38 (JSTOR)