|
En física, la distribució ARGUS, nomenada així per l'experiment de física de partícules ARGUS,[1] és la distribució de probabilitat de la massa invariant reconstruïda d'una partícula en desintegració a sobre d'un fons continu.
Definició
La funció de densitat de probabilitat (fdp) de la distribució ARGUS és:

per a  . On . On  i i  són paràmetres de la distribució, i són paràmetres de la distribució, i

on  i i  són la funció de distribució acumulada i la funció de densitat de probabilitat de la distribució normal estàndard, respectivament. són la funció de distribució acumulada i la funció de densitat de probabilitat de la distribució normal estàndard, respectivament.
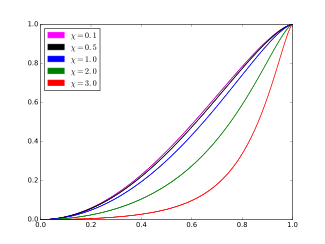
Funció de distribució acumulada
La funció de distribució acumulada (FD) de la distribució ARGUS és
 . .
Estimació de paràmetres
Se suposa que el paràmetre c és conegut (el límit cinemàtic de la distribució de la massa invariant), mentre que χ es pot estimar a partir de la mostra X1, …, Xn utilitzant el principi de màxima versemblança. L'estimador és una funció del segon moment de la mostra i es dona com a solució a l'equació no lineal
 . .
La solució existeix i és única, sempre que el costat dret sigui superior a 0,4; l'estimador resultant  és consistent i asimptòtic normal. és consistent i asimptòtic normal.
Distribució ARGUS generalitzada
De vegades es fa servir una forma més general per a descriure una distribució més en forma de pic:

on Γ(·) és la funció gamma, i Γ(·,·) és la funció gamma incompleta superior.
On els paràmetres c, χ, p representen el tall, curvatura i potència, respectivament.
La moda és

p = 0,5 dona un ARGUS regular, esmentat anteriorment.
Referències
- ↑ Albrecht, H. «Search for hadronic b→u decays» (en anglès). Physics Letters B, 241.2, 1990, pàg. 278–282. Bibcode: 1990PhLB..241..278A. DOI: 10.1016/0370-2693(90)91293-K. (Més formalment per ARGUS Collaboration, H. Albrecht et al.) En aquest article, la funció s'ha definit amb el paràmetre c que representa l'energia del feix i el paràmetre p establert a 0,5. La normalització i el paràmetre χ s'han obtingut a partir de les dades.
Bibliografia
- Albrecht, H. «Measurement of the polarization in the decay B → J/ψK*» (en anglès). Physics Letters B, 340.3, 1994, pàg. 217–220. Bibcode: 1994PhLB..340..217A. DOI: 10.1016/0370-2693(94)01302-0.
- Pedlar, T. ;Cronin-Hennessy, D. ;Hietala, J. ;Dobbs, S. ;Metreveli ,Z. ;Seth ,K. ;Tomaradze ,A. ;Xiao ,T. ;Martin ,L. «Observation of the hc(1P) Using e+e− Collisions above the DD Threshold» (en anglès). Physical Review Letters, 107.4, 2011, pàg. 041803. arXiv: 1104.2025. Bibcode: 2011PhRvL.107d1803P. DOI: 10.1103/PhysRevLett.107.041803. PMID: 21866994.
- Lees, J. P. ;Poireau, V. ;Prencipe, E. ;Tisserand, V. ;Garra Tico, J. ;Grauges, E. ;Martinelli, M. ;Palano, A. ;Pappagallo, M. ;Eigen, G. ;Stugu, B. ;Sun, L. ;Battaglia, M. ;Brown, D. N. ;Hooberman, B. ;Kerth, L. T. ;Kolomensky, Y. G. ;Lynch, G. ;Osipenkov, I. L. ;Tanabe, T. ;Hawkes, C. M. ;Soni, N. ;Watson, A. T. ;Koch, H. ;Schroeder, T. ;Asgeirsson, D. J. ;Hearty, C. ;Mattison, T. S. ;McKenna, J. A. ;Barrett, M. «Search for Charged Lepton Flavor Violation in Narrow Υ Decays» (en anglès). Physical Review Letters, 104.15, 2010, pàg. 151802. arXiv: 1001.1883. Bibcode: 2010PhRvL.104o1802L. DOI: 10.1103/PhysRevLett.104.151802. PMID: 20481982.
|
|---|
| Distribucions discretes
amb suport finit | |
|---|
Distribucions discretes
amb suport infinit | |
|---|
Distribucions contínues
suportades sobre un interval acotat | |
|---|
Distribucions contínues
suportades sobre un interval semi-infinit | |
|---|
Distribucions contínues
suportades en tota la recta real | |
|---|
Distribucions contínues
amb el suport de varis tipus | |
|---|
| Barreja de distribució variable-contínua | |
|---|
| Distribució conjunta | |
|---|
| Direccionals | |
|---|
| Degenerada i singular | |
|---|
| Famílies | |
|---|
|