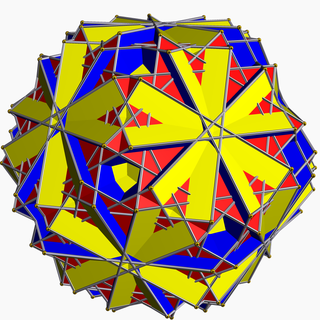
Great truncated icosidodecahedron
Type	Uniform star polyhedron
Elements	F = 62, E = 180 V = 120 (χ = 2)
Faces by sides	30{4}+20{6}+12{10/3}
Coxeter diagram
Wythoff symbol	2 3 5/3 |
Symmetry group	Ih, [5,3], *532
Index references	U68, C87, W108
Dual polyhedron	Great disdyakis triacontahedron
Vertex figure	4.6.10/3
Bowers acronym	Gaquatid

In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U₆₈. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices.^[1] It is given a Schläfli symbol t_0,1,2{⁠5/3⁠,3}, and Coxeter-Dynkin diagram, .

Cartesian coordinates for the vertices of a great truncated icosidodecahedron centered at the origin are all the even permutations of $${\displaystyle {\begin{array}{ccclc}{\Bigl (}&\pm \,\varphi ,&\pm \,\varphi ,&\pm {\bigl [}3-{\frac {1}{\varphi }}{\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,2\varphi ,&\pm \,{\frac {1}{\varphi }},&\pm \,{\frac {1}{\varphi ^{3}}}&{\Bigl )},\\{\Bigl (}&\pm \,\varphi ,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm {\bigl [}1+{\frac {3}{\varphi }}{\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,{\sqrt {5}},&\pm \,2,&\pm \,{\frac {\sqrt {5}}{\varphi }}&{\Bigr )},\\{\Bigl (}&\pm \,{\frac {1}{\varphi }},&\pm \,3,&\pm \,{\frac {2}{\varphi }}&{\Bigr )},\end{array}}}$$

where ${\displaystyle \varphi ={\tfrac {1+{\sqrt {5}}}{2}}}$ is the golden ratio.

Great disdyakis triacontahedron
Type	Star polyhedron
Face
Elements	F = 120, E = 180 V = 62 (χ = 2)
Symmetry group	Ih, [5,3], *532
Index references	DU68
dual polyhedron	Great truncated icosidodecahedron

The great disdyakis triacontahedron (or trisdyakis icosahedron) is a nonconvex isohedral polyhedron. It is the dual of the great truncated icosidodecahedron. Its faces are triangles.

The triangles have one angle of ${\displaystyle \arccos \left({\tfrac {1}{6}}+{\tfrac {1}{15}}{\sqrt {5}}\right)\approx 71.594\,636\,220\,88^{\circ }}$, one of ${\displaystyle \arccos \left({\tfrac {3}{4}}+{\tfrac {1}{10}}{\sqrt {5}}\right)\approx 13.192\,999\,040\,74^{\circ }}$ and one of ${\displaystyle \arccos \left({\tfrac {3}{8}}-{\tfrac {5}{24}}{\sqrt {5}}\right)\approx 95.212\,364\,738\,38^{\circ }.}$ The dihedral angle equals ${\displaystyle \arccos \left({\tfrac {-179+24{\sqrt {5}}}{241}}\right)\approx 121.336\,250\,807\,39^{\circ }.}$ Part of each triangle lies within the solid, hence is invisible in solid models.

• List of uniform polyhedra

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 p. 96

• Weisstein, Eric W. "Great truncated icosidodecahedron". MathWorld.
• Weisstein, Eric W. "Great disdyakis triacontahedron". MathWorld.

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.

• v
• t
• e