|
Couple (physique) En physique et particulièrement en mécanique, un couple est un ensemble de forces de résultante nulle, dont en revanche le moment total n'est généralement pas nul. Le terme « couple » vient du fait que le couple le plus simple est un ensemble de deux forces opposées (de même direction et de même intensité, mais de sens opposés). Le moment d'un couple par rapport à un point ou par rapport à un axe ne dépend pas de la position du point ou de l'axe[note 1]. Le couple tend à initier ou modifier la rotation du système auquel il s'applique (il provoque une variation de son moment cinétique), sans modifier le mouvement de son centre de gravité[1]. La notion de couple est particulièrement importante en mécanique du solide. Dans ce domaine on appelle souvent « couple », par métonymie, le moment du couple (en général, par rapport à un axe). IntroductionLiaison pivot Le couple est au mouvement de rotation ce que la force est au mouvement de translation. Le couple est ce qui provoque une accélération angulaire, et une rotation dans le plan perpendiculaire à la direction du couple[2]. Dans la plupart des cas, on parle de couple pour analyser le mouvement d'une pièce mécanique capable de pivoter autour d'un axe fixe, mais sans degré de liberté dans ses autres mouvements. Une telle liaison mécanique transforme nécessairement en couple toute force extérieure qui lui est appliquée, parce que les points de liaison de l'axe imposent une réaction interne implicite. En pratique, en effet, ces points de liaison de l'axe ajoutent à la pièce mécanique des forces de réaction, induites par le système de force extérieur, ces forces de réaction jouant de telle manière que :
Couple et momentIl y a un rapport direct entre couple et moment, puisque le principal effet d'un couple est de créer un moment, et la manière idéale de créer un moment est de le faire par un couple, mais ce n'est pas la même nature d'objet. On parle de moment d'une force, ou d'un système de forces, pour caractériser l'effet d'une force particulière par rapport à un axe de rotation. Dans ce cas il n'est pas nécessaire de tenir compte de la réaction de la liaison mécanique sur l'axe. Dans un système idéal sans déformation ni frottement, ces forces de réaction ne font en effet qu'équilibrer le système pour que son axe reste fixe ; et elles ne correspondent à aucun travail, elles peuvent donc être négligées dans l'étude dynamique du système. En revanche, il est nécessaire d'en tenir compte pour bien visualiser l'ensemble des forces qui impose un mouvement à un solide : le véritable ensemble de forces extérieures à la pièce est celui qu'il faudrait mettre en place pour obtenir le même mouvement sans que l'axe soit tenu par ses points de fixation, donc en explicitant la réaction implicite de ces fixations. Ce complément étant apporté, il est possible d'étudier le mouvement de la pièce uniquement soumise à un ensemble de forces et sans liaison mécanique : cet ensemble de forces (y compris donc les forces de réaction sur l'axe) réalise un couple. En réalité, le couple n'existe pas intrinsèquement. Il est toujours associé à un ensemble de forces s'annulant vectoriellement mais dont les moments s'ajoutent sans s'annuler. C'est par exemple le résultat de l'action du vent sur une éolienne, ou l'action des forces électromagnétiques sur le rotor d'un moteur électrique. Fondamentalement, un moment est une grandeur physique pseudovectorielle tandis qu'un couple est la résultante d'une distribution de forces dont la somme vectorielle est nulle. Ce n'est donc pas le couple qui est la grandeur physique, mais le moment de ce couple. Dans l'analogie entre rotation et translation, l'analogue d'une force n'est donc en fait ni un « couple » ni un « moment », mais en toute rigueur le moment créé par un couple. En pratique, lorsque le contexte ne prête pas à confusion, on qualifie souvent de « couple » ce qui est en réalité le « moment du couple résultant ». Couple de serrageEn mécanique auto, le couple de serrage est mesuré à l'aide d'une clef dynamométrique. Effet d'une force sur un solide En mécanique du solide, une force appliquée dans le cas général sur un point P à une distance du centre de gravité O d'un solide, provoque à la fois une accélération linéaire, et une accélération angulaire du solide. On montre (en étudiant l'égalité des sommes et des moments des forces) que cet effet peut être décomposé en deux effets indépendants[2] :
Inversement, un « couple de forces » formé de deux forces et , d'intensité égales et de sens opposés, s'exerçant dans un plan en deux points séparés d'une distance , conduit à une accélération angulaire mais n'entraîne pas d'accélération linéaire. On peut montrer que le moment global d'un tel couple par rapport à n'importe quel point est alors égal au produit vectoriel constant, caractéristique du couple : Notation du couple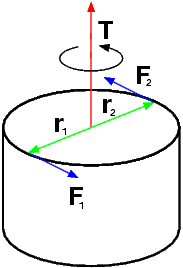 On appelle « couple » tout ensemble de forces dont la résultante sur le système est nulle et le moment résultant par rapport à un point est non nul. Dans le cas général, le moment d'un système de force par rapport à un point A est égal au moment de ce système par rapport à un point O, plus le produit vectoriel du vecteur par la résultante des forces.
Le couple étant un système d'actions mécaniques dont la résultante est nulle, son moment résultant est indépendant du point choisi pour le calculer : On utilise souvent la notation pour représenter le moment résultant d'un couple. Compte tenu du résultat précédent, il n'est en effet pas nécessaire de préciser le point choisi pour calculer le moment. On représente un couple par une flèche (semblable à celle qui représente un vecteur) perpendiculaire au plan d'application des forces, s'éloignant de l'objet pour une rotation dans le sens trigonométrique (qui est l'inverse du sens des aiguilles d'une montre), comme la vitesse de rotation. Représentation d'un coupleIl existe une infinité de représentations différentes d'un même couple donné. Un couple peut toujours être remplacé par un autre de même moment et de même direction, dont l'intensité des forces ou l'écart des points d'application peut être fixé à volonté, du moment que le produit des deux respecte celui du couple initial[2]. Cet effet commun à tous les « couples de force » équivalents est celui d'un « couple », abstraction faite de la paire particulière de forces capable de le créer (ou même de toute autre collection vectorielle coplanaire à somme nulle qui aurait le même effet). Le « couple » est (par définition) le produit vectoriel associé à un tel « couple de forces », ou de manière équivalente, la somme des produits moments de ces forces par rapport à un point quelconque. Outre les autres cas évidents, le couple est nul lorsque les deux forces ont la même droite d'action. Le couple augmente avec l'intensité commune des forces, mais aussi avec l'éloignement des points. Il est maximal lorsque et sont orthogonaux. Représentation la plus simpleLa plus simple, qui lui donne son nom, consiste à considérer un ensemble de deux forces :
Ainsi, la résultante est bien nulle. On suppose de plus que les vecteurs et ne sont pas colinéaires au vecteur ; le cas le plus simple consiste à prendre les deux forces perpendiculaires à ce vecteur :  Si on note la distance , la norme des forces , et le vecteur unitaire perpendiculaire au plan de la figure, le couple vaut explicitement : Exemples d'autres représentationsOn peut représenter le même couple que dans l'exemple précédent par d'autres ensembles d'actions mécaniques. Par exemple, par deux forces :
Ainsi, la résultante est toujours nulle. Pour simplifier, on peut encore supposer que les vecteurs et sont perpendiculaires au vecteur :  Pour retrouver la même valeur du couple : , il suffit de prendre par exemple une combinaison du type :
Il existe une infinité de représentations possibles. Théorème de VarignonLe moment en de la résultante de plusieurs forces concourantes en un même point est égal à la somme des moments en de ces différentes forces : avec . En effet : En aucun cas il n'est possible de déduire que « somme des moments = moment de la somme ». Cela n'est vrai que pour un ensemble de forces appliquées au même point. Cela montre enfin qu'une action mécanique n'est pas représentable par un seul vecteur force. La considération du point d'application est primordiale. Notes et références
Notes
Références
Voir aussiArticles connexesLien externe
|










































