|
Квантовый ластикЭксперимент квантового ластика — интерференционный эксперимент, который демонстрирует квантовую запутанность и принцип дополнительности. Эксперимент с квантовым ластиком на двух щелях, описываемый в данной статье, состоит из трёх стадий[1]:
Основной результат эксперимента заключается в том, что не имеет значения, был процесс стирания выполнен до или после того, как фотоны достигли экрана детектора[1][2]. Технологию квантового стирания можно использовать для увеличения разрешающей способности современных микроскопов[3]. ВведениеЭксперимент квантового ластика, описываемый в данной статье, является вариацией классического опыта Юнга на двух щелях, который устанавливает, что фотон не может интерферировать с самим собой при попытке экспериментатора определить, через какую именно щель прошёл фотон. Когда поток фотонов подвергается подобному наблюдению, характерные для опыта Юнга интерференционные полосы не наблюдаются. Эксперимент квантового ластика способен создать ситуации, при которых фотон, который был «промаркирован» для определения, через какую именно щель он прошёл, впоследствии может быть «очищен» от такой маркировки. «Промаркированный» фотон не может интерферировать с самим собой и не будет порождать интерференционные полосы, но фотон, который был «промаркирован» и затем «очищен», может впоследствии интерферировать с самим собой и будет способствовать порождению интерференционных полос, аналогичных полученным в ходе опыта Юнга[1]. Эксперимент квантового ластика использует установку с двумя основными секциями. После создания двух запутанных фотонов каждый из них направляется в свою секцию. Все действия по определению пути одного из запутанных фотонов (изучаемого в секции с двумя щелями) будут оказывать влияние на второй фотон и наоборот. Преимущество манипулирования парой запутанных фотонов заключается в том, что экспериментаторы могут разрушить или восстановить интерференционную картину без внесения изменений в ту секцию установки, которая содержит пластину с двумя щелями. Экспериментаторы добиваются этого за счёт манипулирования запутанным фотоном, и такая манипуляция может быть выполнена до или после того, как одна из запутанных частиц прошла сквозь щели и другие элементы установки между источником фотонов и экраном детектора. То есть, в условиях, когда секция с двумя щелями была собрана таким образом, чтобы предотвратить проявление феномена интерференции (вследствие наличия информации о выбранном пути следования фотона), квантовый ластик может быть использован для фактического стирания этой информации. При использовании этой возможности, экспериментатор восстанавливает интерференцию без внесения изменений в ту секцию установки, которая содержит две щели[1]. Один из вариантов этого эксперимента, квантовый ластик с отложенным выбором, позволяет принять решение сохранить или уничтожить информацию о выбранном пути уже после того как одна из запутанных частиц (та, которая проходит сквозь щели) проинтерферирует (или не проинтерферирует) с самой собой[4]. В таком эксперименте квантовые эффекты могут имитировать влияние будущих действий на события в прошлом. Однако, временной порядок измерений в данном случае не имеет значения[5]. Эксперимент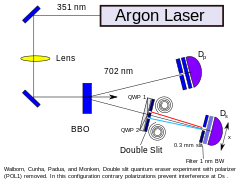 Вначале фотон пропускается через специальное нелинейное оптическое устройство: кристал бета-бората бария[англ.] (BBO). Этот кристал преобразует единичный фотон в пару запутанных фотонов пониженной частоты, процесс известен как спонтанное параметрическое рассеяние. Эти запутанные фотоны следуют разными путями: один фотон движется прямо к детектору, в то время как второй проходит через двухщелевую пластину на второй детектор. Оба детектора подключены к схеме совпадений, гарантирующей, что будут учтены только запутанные фотоны. Шаговый двигатель перемещает второй детектор вдоль сканируемой области, формируя карту интенсивности. Такая конфигурация порождает знакомую интерференционную картину. 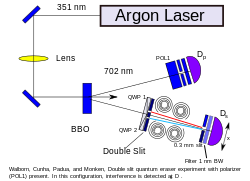 Далее, перед каждой прорезью в двухщелевой пластине помещается круговой поляризатор, выполняя поляризацию по часовой стрелке для света, проходящего через одну щель, и против часовой стрелки для света, проходящего через другую щель (см. рис. 1). Эта поляризация регистрируется на детекторе, «маркируя» таким образом фотоны и разрушая интерференционную картину (см. законы Френеля-Араго[англ.]). Наконец, линейный поляризатор устанавливается на пути первого запутанного фотона из пары, придавая ему диагональную поляризацию (см. рис. 2). Запутанность гарантирует дополнительную диагональную поляризацию у второго фотона, который проходит через двухщелевую пластину. Это нивелирует влияние круговых поляризаторов: каждый фотон будет давать смесь света, поляризованного по часовой стрелке и против неё. Следовательно, второй детектор больше не может определить, какой именно путь был выбран, и интерференционная картина восстанавливается. Эксперимент с двойной щелью и круговыми поляризаторами также может быть описан при рассмотрении света как классической волны[6]. Однако эксперимент квантового ластика использует запутанные фотоны, которые не совместимы с классической механикой. Распространенные заблужденияРаспространенное заблуждение относительно этого эксперимента состоит в том, что его можно использовать для мгновенной передачи информации между двумя детекторами. Однако простая причинно-следственная связь исключает навязывание «заданной» информации в наблюдаемых результатах. В этой экспериментальной установке важно понимать роль схемы (детектора) совпадений. Линейный поляризатор в верхнем пути отфильтровывает половину запутанных фотонов, а через детектор совпадений отфильтровываются соответствующие фотоны в нижнем пути. Детектор совпадений может работать только путем сравнения данных с обоих датчиков, что делает невозможным использование этой установки для мгновенной связи. Другими словами, лишь небольшой процент света, проходящего через кристалл BBO, расщепляется на запутанные пары. Подавляющее большинство фотонов, проходящих через кристалл, не расщепляются и должны быть удалены из конечного набора данных как нежелательный шум. Поскольку у детекторов нет возможности определить, был ли пойманный фотон частью запутанной пары, то решение принимается путем просмотра таймингов (моментов времени) и фильтрации любых фотонов, которые не были захвачены в то же время, что и их парный фотон на другом детекторе. Таким образом, когда создается пара запутанных фотонов, но один из них блокируется поляризатором и теряется, то его парный фотон будет отфильтрован из результирующего набора данных, как если бы он был не запутанным фотоном. При таком рассмотрении неудивительно, что внесение изменений в верхний путь может повлиять на измерения, сделанные в нижнем пути, поскольку сравниваются два результата измерения, которые затем используются для фильтрации данных. Обратите внимание, что в конечном состоянии этой экспериментальной установки измерения на нижнем пути всегда показывают размытую картину для необработанных данных. Увидеть интерференционную картину можно только путем фильтрации данных с помощью детектора совпадений и просмотра только тех фотонов, которые составляют половину запутанной пары. См. такжеСсылки
Примечания
|