自编码器

此條目可参照英語維基百科相應條目来扩充。 若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。

机器学习与数据挖掘
范式 监督学习 無監督學習 線上機器學習 元学习（英语：Meta-learning (computer science)） 半监督学习 自监督学习 强化学习 基于规则的机器学习（英语：Rule-based machine learning） 量子機器學習
问题 统计分类 生成模型 迴歸分析 聚类分析 降维 密度估计（英语：density estimation） 异常检测 数据清洗 自动机器学习 关联规则学习 語意分析 结构预测（英语：Structured prediction） 特征工程 表征学习 排序学习（英语：Learning to rank） 语法归纳（英语：Grammar induction） 本体学习（英语：Ontology learning） 多模态学习
监督学习 (分类 · 回归) 学徒学习（英语：Apprenticeship learning） 决策树学习 集成学习 Bagging 提升方法 随机森林 k-NN 線性回歸 朴素贝叶斯 人工神经网络 邏輯斯諦迴歸 感知器 相关向量机（RVM） 支持向量机（SVM） 迁移学习 微调
聚类分析 BIRCH CURE算法（英语：CURE algorithm） 层次 k-平均 Fuzzy 期望最大化（EM） DBSCAN OPTICS 均值飘移（英语：Mean shift）
降维 因素分析 CCA ICA LDA NMF（英语：Non-negative matrix factorization） PCA PGD（英语：Proper generalized decomposition） t-SNE（英语：t-distributed stochastic neighbor embedding） SDL
结构预测（英语：Structured prediction） 圖模式 貝氏網路 條件隨機域 隐马尔可夫模型
异常检测 RANSAC k-NN 局部异常因子（英语：Local outlier factor） 孤立森林（英语：Isolation forest）
人工神经网络 自编码器 認知計算 深度学习 DeepDream（英语：DeepDream） 多层感知器 RNN LSTM GRU（英语：Gated recurrent unit） ESN（英语：Echo state network） 储备池计算（英语：reservoir computing） 受限玻尔兹曼机 GAN SOM CNN U-Net Transformer Vision transformer（英语：Vision transformer） 脉冲神经网络（英语：Spiking neural network） Memtransistor（英语：Memtransistor） 电化学RAM（英语：Electrochemical RAM）（ECRAM）
强化学习 Q学习 SARSA 时序差分（TD） 多智能体（英语：Multi-agent reinforcement learning） Self-play（英语：Self-play (reinforcement learning technique)） RLHF
与人类学习 主动学习（英语：Active learning (machine learning)） 众包 Human-in-the-loop（英语：Human-in-the-loop）
模型诊断 学习曲线（英语：Learning curve (machine learning)）
数学基础 内核机器（英语：Kernel machines） 偏差–方差困境（英语：Bias–variance tradeoff） 计算学习理论（英语：Computational learning theory） 经验风险最小化 奥卡姆学习（英语：Occam learning） PAC学习（英语：Probably approximately correct learning） 统计学习 VC理论
大会与出版物 NeurIPS ICML（英语：International Conference on Machine Learning） ICLR ML（英语：Machine Learning (journal)） JMLR（英语：Journal of Machine Learning Research）
相关条目 人工智能术语（英语：Glossary of artificial intelligence） 机器学习研究数据集列表（英语：List of datasets for machine-learning research） 机器学习概要（英语：Outline of machine learning）
查 论 编

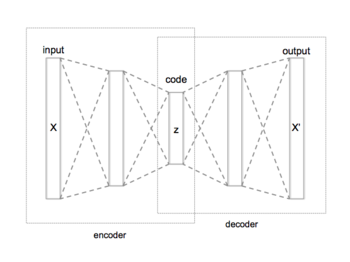
自编码器（英語：autoencoder）也称自动编码器，是一种人工神经网络，用于学习无标签数据的有效编码；属一种无监督学习。

自编码（autoencoding）的目的是：学习对高维度数据做低维度“表示”（“表征”或“编码”）；因此， 通常用于降维。最近，自编码的概念广泛地用于数据的生成模型。^[1][2] 自2010年以来，一些先进的人工智能在深度学习网络中采用了采用堆叠式稀疏自编码。^[3]

自编码器有两个主要部分组成：编码器用于将输入编码，而解码器使用编码重构输入。

实现这个功能最简单的方式就是重复原始信号。然而，自编码器通常被迫近似地重构输入信号，重构结果仅仅包括原信号中最相关的部分。

自编码器的思想已经流行了几十年，其首次应用可以追溯到20世纪80年代。^[4][5][6]自编码器最传统的应用是降维或特征学习，现在这个概念已经推广到用于学习数据的生成模型。.^[1][2]21世纪10年代的一些最强大的人工智能在深度神经网络中采用了自编码器。^[3]

最简单的自编码器形式是一个前馈的、非循环的神经网络，用一层或多层隐藏层链接输入和输出。输出层节点数和输入层一致。其目的是重构输入（最小化输入和输出之间的差异），而不是在给定输入的情况下预测目标值，所以自编码器属于无监督学习。

最简单的自编码器形式是一个前馈的、非循环的神经网络，类似于多层感知器（MLP）中的单层感知器，用一层或多层隐藏层链接输入和输出。输出层具有与输入层相同数量的节点（神经元）。输出层节点数和输入层一致。其目的是重构输入（最小化输入和输出之间的差异），而不是在给定输入${\displaystyle X}$的情况下预测目标值${\displaystyle Y}$， 所以自编码器属于无监督学习。

自编码器由编码器和解码器组成，二者可以被分别定义为变换 ${\displaystyle \phi }$ 和${\displaystyle \psi }$ ，使得：

${\displaystyle \phi :{\mathcal {X}}\rightarrow {\mathcal {F}}}$

${\displaystyle \psi :{\mathcal {F}}\rightarrow {\mathcal {X}}}$

${\displaystyle \phi ,\psi ={\underset {\phi ,\psi }{\operatorname {arg\,min} }}\,\|{\mathcal {X}}-(\psi \circ \phi ){\mathcal {X}}\|^{2}}$

在最简单的情况下，给定一个隐藏层，自编码器的编码阶段接受输入${\displaystyle \mathbf {x} \in \mathbb {R} ^{d}={\mathcal {X}}}$并将其映射到${\displaystyle \mathbf {h} \in \mathbb {R} ^{p}={\mathcal {F}}}$：

${\displaystyle \mathbf {h} =\sigma (\mathbf {Wx} +\mathbf {b} )}$

像${\displaystyle \mathbf {h} }$通常表示编码、潜变量或潜在表示。${\displaystyle \sigma }$是一个逐元素的激活函数（例如sigmoid函数或线性整流函数）。${\displaystyle \mathbf {W} }$是权重矩阵，${\displaystyle \mathbf {b} }$是偏置向量。权重和偏置通常随机初始化，并在训练期间通过反向传播迭代更新。自编码器的解码阶段映射${\displaystyle \mathbf {h} }$到重构${\displaystyle \mathbf {x'} }$（与${\displaystyle \mathbf {x} }$形状一致）：

${\displaystyle \mathbf {x'} =\sigma '(\mathbf {W'h} +\mathbf {b'} )}$

其中解码器部分的${\displaystyle \mathbf {\sigma '} ,\mathbf {W'} ,\mathbf {b'} }$ 可能与编码器部分的${\displaystyle \mathbf {\sigma } ,\mathbf {W} ,\mathbf {b} }$无关。

自编码器被训练来最小化重建误差（如平方误差），通常被称为 "损失"：

${\displaystyle {\mathcal {L}}(\mathbf {x} ,\mathbf {x'} )=\|\mathbf {x} -\mathbf {x'} \|^{2}=\|\mathbf {x} -\sigma '(\mathbf {W'} (\sigma (\mathbf {Wx} +\mathbf {b} ))+\mathbf {b'} )\|^{2}}$

其中${\displaystyle \mathbf {x} }$通常在训练集上平均。

如前所述，和其它前馈神经网络一样，自编码器的训练是通过误差的反向传播进行的。

当特征空间${\displaystyle {\mathcal {F}}}$的维度比输入空间${\displaystyle {\mathcal {X}}}$低时，特征向量${\displaystyle \phi (x)}$可以看作时输入${\displaystyle x}$的压缩表示，这就是不完备自动编码（undercomplete autoencoders）的情况。如果隐藏层大于（过完备）或等于输入层的数量，或者隐藏单元的容量足够大，自编码器就可能学会恒等函数而变得无用。然而，实验结果表明过完备自编码器（overcomplete autoencoders）仍然可能学习到有用的特征。^[7]在理想情况下，编码的维度和模型容量可以根据待建模数据分布的复杂性来设定，采用这种方式的一种途径是正则化自编码器。^[4]

• 表征学习