一種物質的蒸氣壓 也称作飽和蒸氣壓 ,指的是這種物质的气相 与其非气相达到平衡状态时的压强 ;任何物质(包括液态 与固态 )都有挥发 成为气态的趋势,其气态也同样具有凝結 为液态或者凝华 为固态的趋势。在给定的温度下,一种物质的气态与其凝聚态 (固态或液态)之间会在某一个压强下存在动态平衡。此时单位时间内由气态转变为凝聚态的分子 数与由凝聚态转变为气态的分子数相等。这个压强就是此物质在此温度下的饱和蒸气压。
在密閉空間 ,物質在給定的溫度 下,可使該物質沸騰的氣體分壓 ,此时蒸发 /凝结过程达到动态平衡 。当气体的压力(分压)与饱和蒸汽压相等时,对应的温度称为露点 ,这时空气的相对湿度为100%。此时如果降低温度或者增加空气中水蒸气的含量,就会出现水凝结的现象。
它们之间的关系可以用克劳修斯-克拉佩龙方程 (Clausius–Clapeyron relation)描述[ 1] 沸腾 ,而这个温度叫做此压强下的沸点 。物质的常压沸点就是此物质的饱和蒸气压等于一个标准大气压 时候的温度。需要注意的是在较深液体中发生的沸腾所需温度会高于较浅液体中的沸腾,因为除了大气压强外还需要克服液体自身深度所造成的压强。對於溶液 ,計算需用拉午耳定律 [ 2]
水的饱和蒸汽压可以根据Goff-Gratch方程式 确定。
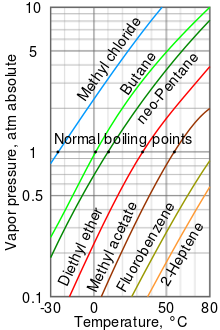
數種不同的液體的蒸氣壓力 對比。
安托萬方程 [ 3] [ 4]
log
P
=
A
−
B
C
+
T
{\displaystyle \log P=A-{\frac {B}{C+T}}}
將溫度項單獨移至等號左邊後可得:
T
=
B
A
−
log
P
−
C
{\displaystyle T={\frac {B}{A-\log P}}-C}
其中:
P
{\displaystyle P}
T
{\displaystyle T}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
而上式在某些情況項又可以被化簡為如下:
T
=
B
A
−
log
P
{\displaystyle T={\frac {B}{A-\log P}}}
總體來說,安托萬方程的使用上有許多限制。例如,該方程無法找出一組可適用於熔點與臨界溫度的範圍內的
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
托 下的低壓環境也相當不精準。
^ Clausius-Clapeyron Equation . Chemistry LibreTexts. 2014-06-01 [2024-02-16 ] . (原始内容存档 于2021-04-15) (英语) . ^ Raoult's Law . Chemistry LibreTexts. 2013-10-02 [2024-02-16 ] . (原始内容存档 于2024-02-16) (英语) . ^ Coulson, J. M.; Richardson, J. F.; Sinnott, Raymond K. Chemical engineering. 6: Chemical engineering design. Chemical Engineering Design 4. ed. Amsterdam Heidelberg: Elsevier. 2005: 331. ISBN 978-0-7506-6538-4 ^ Antoine's Equation . uweb.engr.arizona.edu. [2024-02-16 ] . (原始内容存档 于2024-02-16).