Grup polihedral

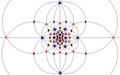
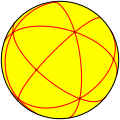
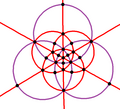
Grup titik dalam tiga dimensi

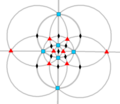
Simetri involusi Cs, (*) [ ] =	Simetri siklik Cnv, (*nn) [n] =	Simetri dihedral Dnh, (*n22) [n,2] =
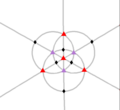
Grup polihedral, [n,3], (*n32)
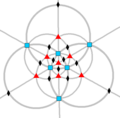
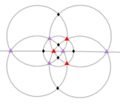
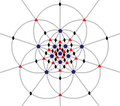
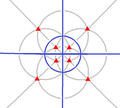
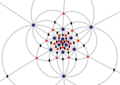
Simetri tetrahedral Td, (*332) [3,3] =	Simetri oktahedral Oh, (*432) [4,3] =	Simetri ikosahedral Ih, (*532) [5,3] =

Dalam geometri, grup polihedral adalah salah satu dari grup simetri dari padatan Platonis.

Ada tiga grup polihedral:

• Grup tetrahedral urutan 12, grup simetri rotasi dari tetrahedron beraturan. Ini isomorfik untuk A₄.
  • Kelas konjugasi dari T adalah:
    • identitas
    • 4 × rotasi sebesar 120°, urutan 3, cw
    • 4 × rotasi sebesar 120°, urutan 3, ccw
    • 3 × rotasi 180°, urutan 2
• Grup oktahedral urutan 24, grup simetri rotasi kubus dan oktahedron beraturan. Ini isomorfik untuk S₄.
  • Kelas konjugasi dari O adalah:
    • identitas
    • 6 × rotasi sebesar ±90° di sekitar simpul, urutan 4
    • 8 × rotasi ±120° di sekitar pusat segitiga, urutan 3
    • 3 × rotasi 180° di sekitar simpul, urutan 2
    • 6 × rotasi 180° di sekitar titik tengah tepi, urutan 2
• Grup ikosahedral urutan 60, grup simetri rotasi dari dodecahedron beraturan dan ikosahedron beraturan. Ini isomorfik untuk A₅.
  • Kelas konjugasi dari I adalah:
    • identitas
    • 12 × rotasi sebesar ±72°, urutan 5
    • 12 × rotasi sebesar ±144°, urutan 5
    • 20 × rotasi sebesar ±120°, urutan 3
    • 15 × rotasi 180°, urutan 2

Simetri lipatan menjadi 24, 48, 120 untuk grup refleksi penuh. Simetri pantulan memiliki 6, 9, dan 15 cermin. Simetri oktahedral, [4,3] dilihat sebagai gabungan dari 6 simetri tetrahedral [3,3] cermin, dan 3 cermin simetri dihedral Dih₂, [2,2 ]. Simetri piritohedral adalah penggandaan lain dari simetri tetrahedral.

Kelas konjugasi simetri tetrahedral penuh, T_d≅S₄, adalah:

• identitas
• 8 × rotasi sebesar 120°
• 3 × rotasi 180°
• 6 × refleksi dalam bidang melalui dua sumbu rotasi
• 6 × rotorefleksi sebesar 90°

Kelas konjugasi simetri piritohedral, T_h, termasuk kelas T, dengan dua kelas 4 digabungkan, dan dengan inversi:

• identitas
• 8 × rotasi 120°
• 3 × rotasi 180°
• inversi
• 8 × rotorefleksi sebesar 60°
• 3 × refleksi dalam bidang

Kelas konjugasi dari grup oktahedral penuh, O_h≅S₄ × C₂, adalah:

• inversion
• 6 × rotorefleksi sebesar 90°
• 8 × rotorefleksi sebesar 60°
• 3 × refleksi pada bidang tegak lurus terhadap sumbu lipatan-4
• 6 × refleksi pada bidang yang tegak lurus terhadap sumbu lipatan-2

Kelas konjugasi simetri ikosahedral penuh, I_h≅A₅ × C₂, sertakan juga dengan inversi:

• inversi
• 12 × rotorefleksi sebesar 108°, urutan 10
• 12 × rotorefleksi sebesar 36°, urutan 10
• 20 × rotorefleksi sebesar 60 °, urutan 6
• 15 × refleksi, urutan 2

Grup polihedral kiral

Nama (Orb.)	Notasi Coxeter	Urutan	Struktur abstrak	Rotasi Titik #valensi	Diagram
					Orthogonal	Stereografis
T (332)	[3,3]+	12	A4	43 32
Th (3*2)	[4,3+]	24	A4×2	43 3*2
O (432)	[4,3]+	24	S4	34 43 62
I (532)	[5,3]+	60	A5	65 103 152	120px

Grup polihedral penuh

Weyl Schoe. (Orb.)	Notasi Coxeter	Urutan	Struktur abstrak	Bilangan Coxeter (h)	Cermin (m)	Diagram cermin
						Ortogonal	Stereografis
A3 Td (*332)	[3,3]	24	S4	4	6
B3 Oh (*432)	[4,3]	48	S4×2	8	3 6
H3 Ih (*532)	[5,3]	120	A5×2	10	15

• Simbol Wythoff
• Daftar grup simetri bola

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, 1973. (The Polyhedral Groups. §3.5, pp. 46–47)

• Weisstein, Eric W. "PolyhedralGroup". MathWorld.