|
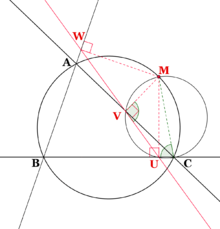
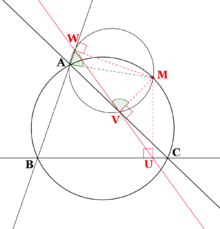
Droite de Simson Soit un triangle ABC, M un point du plan et U, V et W les projetés orthogonaux de M sur les droites (BC), (AC) et (AB). Alors les deux propositions suivantes sont équivalentes :
Dans ce cas, la droite portant les points U, V et W s'appelle la droite de Simson (ou droite de Wallace, qui fut en fait le premier à la découvrir en 1799) associée au point M. En particulier :
Diverses propriétésSi H est l'orthocentre du triangle ABC, alors la droite MH et la droite de Simson associée à M se coupent sur le cercle d'Euler du triangle ABC. Si M et M' sont deux points du cercle circonscrit, alors l'angle entre les droites de Simson de ces deux points est la moitié de l'arc MM'. En particulier, si M et M' sont diamétralement opposés sur le cercle leurs droites de Simson sont perpendiculaires et en outre leur point d'intersection se trouve sur le cercle d'Euler du triangle. Deux triangles étant donnés, inscrits dans le même cercle, les deux droites de Simson d'un point M par rapport aux deux triangles font entre elles un angle constant, qui ne dépend pas du choix du point M. Enveloppe des droites de SimsonThéorème — L'enveloppe des droites de Simson d'un triangle est une deltoïde.  L'article consacré à la deltoïde de Steiner présente ses propriétés. Voir aussiArticles connexesLiens externes
Information related to Droite de Simson |