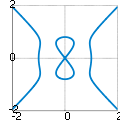
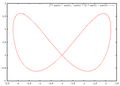
Lemniscate

Une lemniscate est une courbe plane ayant la forme d'un 8. Elle possède deux axes de symétrie perpendiculaires. Ceux-ci se coupent en un point double de la courbe, également son centre de symétrie.

La lemniscate est connue depuis l'Antiquité grecque ; Persée, étudiant les spiriques, la définissait comme la section par un plan du volume formé par la rotation d'un cercle autour d'un axe tangentiel (soit un tore de rayon intérieur nul)^[1].

La première lemniscate dont on ait exprimé la formule analytique, celle « de Bernoulli », fait partie de la famille des ovales de Cassini, décrits par Giovanni Domenico Cassini en 1680. Elle fut redécouverte en 1694 par Jacques Bernoulli lors de ses travaux sur l'ellipse et ses variations^[2], et baptisée lemniscus (« ruban » en latin), mot tiré du grec λημνίσκος, lèmnískos, bandelette. La lemniscate de Bernoulli est souvent appelée simplement « lemniscate ».

On a pu penser que le symbole de l'infini (∞) provenait de la lemniscate de Bernoulli, mais la première utilisation de ce symbole remonte au moins à John Wallis en 1655^[3],[4],[5] (soit 40 ans avant la description de Bernoulli), et lui est même sans doute antérieure (voir l'article Infini).

Si l'on prend pour axe des abscisses la droite joignant les deux sommets, et pour axe des ordonnées son autre axe de symétrie, l'équation d'une lemniscate peut s'écrire :

${\displaystyle y=\pm \,a\,f\!\left({\frac {x}{a}}\right)}$

où a désigne une constante et f une fonction paire définie sur l'intervalle [–1,+1], vérifiant f(0) = f(1) = 0 et présentant un unique maximum sur l'intervalle ]0,1[.

Cette formule générale explicitant y n'est souvent pas, cependant, la façon la plus simple de représenter une lemniscate. Pour celle de Bernoulli, par exemple, la formule explicite est :

${\displaystyle y=\pm \,{\frac {a}{\sqrt {2}}}\,{\sqrt {{\sqrt {1+8\left({\frac {x}{a}}\right)^{2}}}-\left[1+2\left({\frac {x}{a}}\right)^{2}\right]}}~~(|x|\leq a)}$

alors que l'équation implicite est plus commode à manipuler :

${\displaystyle (x^{2}+y^{2})^{2}=a^{2}(x^{2}-y^{2}).}$

Lemniscates les plus usuelles :

• lemniscate de Bernoulli, la plus classique ;
• lemniscate de Gerono, en fait une courbe de Lissajous ;
• lemniscates de Booth, une généralisation du cas précédent ;
• courbe du diable ;
• besace ;
• symbole de l'infini ;
• transformée d'une hyperbole par une inversion.

• Divers exemples de lemniscates
• 
  Lemniscate de Bernoulli.
• 
  Lemniscate de Gerono.
• 
  Lemniscates de Booth.
• 
  Une courbe du diable.
• 
  Besace.
• 
  Exemple d'analemme.

• Les « constantes de la lemniscate » sont deux nombres L₁ et L₂, calculés par Gauss, qui interviennent dans le calcul de la longueur d'une lemniscate de Bernoulli.

• André Rondenay, polytechnicien et délégué militaire de la région de Paris en 1944, avait choisi « Lemniscate » comme pseudonyme^[6].

• Analemme, figure en forme de huit (positions du soleil dans le ciel au cours d’une année, à la même heure et au même endroit)

• Lemniscate, sur MathCurve.

• Portail de la géométrie