O teste de esfericidade de Mauchly ou W de Mauchly é um teste estatístico usado para validar uma análise de variância de medidas repetidas (ANOVA). Foi desenvolvido em 1940 por John Mauchly.

A esfericidade é uma suposição importante de uma ANOVA de medidas repetidas. É a condição em que as variâncias das diferenças entre todos os pares possíveis de condições dentro do sujeito (ou seja, níveis da variável independente) são iguais. A violação da esfericidade ocorre quando não é o caso de as variâncias das diferenças entre todas as combinações das condições serem iguais. Se a suposição de esfericidade for violada, os cálculos de variância podem ser distorcidos, o que resultaria em uma razão F inflada.^[1] A esfericidade pode ser avaliada quando há três ou mais níveis de um fator de medida repetida e, a cada fator de medida repetida adicional, o risco de violação da esfericidade aumenta. Se a esfericidade for violada, deve-se decidir se uma análise univariada ou multivariada é selecionada. Se um método univariado for selecionado, a ANOVA de medidas repetidas deve ser corrigida adequadamente dependendo do grau em que a esfericidade foi violada.^[2]

Desenvolvido em 1940 por John W. Mauchly,^[3] o teste de esfericidade de Mauchly é um teste popular para avaliar se a suposição de esfericidade foi violada. A hipótese nula (de esfericidade) e a hipótese alternativa (de não esfericidade) podem ser escritas matematicamente em termos de pontuações de diferença.

Interpretar o teste de Mauchly é bastante simples. Quando a probabilidade da estatística de teste de Mauchly for maior ou igual a ${\displaystyle \alpha }$ (ou seja, p > ${\displaystyle \alpha }$, com ${\displaystyle \alpha }$ comumente definido como 0,05), deixamos de rejeitar a hipótese nula de que as variâncias são iguais. Portanto, podemos concluir que a suposição não foi violada. No entanto, quando a probabilidade da estatística de teste de Mauchly for menor ou igual a ${\displaystyle \alpha }$ (ou seja, p < ${\displaystyle \alpha }$ ), a esfericidade não pode ser presumida e, portanto, concluiríamos que existem diferenças significativas entre as variâncias das diferenças.^[4] A esfericidade é sempre atendida para dois níveis de um fator de medida repetida e, portanto, não é necessário avaliar.^[1]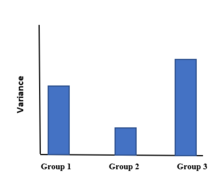

Quando a esfericidade for estabelecida, a razão F é válida e, portanto, interpretável. No entanto, se o teste de Mauchly for significativo, as razões F produzidas devem ser interpretadas com cautela, pois as violações dessa suposição podem resultar em um aumento na taxa de erro do Tipo I e influenciar as conclusões extraídas de sua análise.^[4] Nos casos em que o teste de Mauchly é significativo, modificações precisam ser feitas nos graus de liberdade para que uma razão F válida possa ser obtida.

No SPSS, três correções são geradas: a correção de Greenhouse-Geisser (1959), a correção de Huynh-Feldt (1976) e o limite inferior. Cada uma dessas correções foi desenvolvida para alterar os graus de liberdade e produzir uma razão F onde a taxa de erro do Tipo I é reduzida. A relação F real não muda como resultado da aplicação das correções; apenas os graus de liberdade.^[4]

Um procedimento alternativo é usar a estatística de teste multivariada (MANOVA), uma vez que não requer a suposição de esfericidade.^[5] No entanto, esse procedimento pode ser menos poderoso do que usar uma ANOVA de medidas repetidas, especialmente quando a violação de esfericidade não é grande ou os tamanhos das amostras são pequenos.^[6]

Embora o teste de Mauchly seja um dos mais comumente usados para avaliar a esfericidade, o teste não detecta desvios da esfericidade em amostras pequenas e exagera na detecção de desvios da esfericidade em amostras grandes. Consequentemente, o tamanho da amostra tem influência na interpretação dos resultados.^[4] Na prática, é extremamente improvável que a suposição de esfericidade seja exatamente atendida, portanto, é prudente corrigir uma possível violação sem realmente testar uma violação.