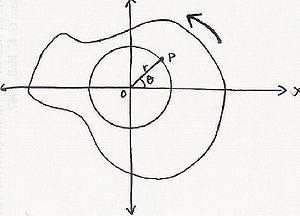
 刚体上一点 P 绕一固定轴的转动。
刚体上一点 P 绕一固定轴的转动。
在物理學中,角移(angular displacement)亦稱為角位移,是一種物理量,用來描述一质点或物体绕某一轴所转过的角度,無单位。角位移有大小和方向,但不满足平行四边形合成法则,所以一般不是向量。[1][2]无限小的角位移是矢量,其方向满足右手螺旋法则。[3]
若一質點在固定的圓上繞圓心運動,因質點與圓心的距離恆不變,即是半徑,因此質點在圓周上的位移可以使用角度變化來描述,而質點繞圓心旋轉所形成的角度變化稱為角移或角位移。[4]
右图为刚体上一点 P,距离原点 r,绕一固定在原点的轴转动。在极坐标系中,P点的坐标为 (r, θ)。一段时间内,P点走过的弧长s与角位置的关系为:

则角位移为:

如果物体从P点转到Q点,两点的角坐标分别是 和
和 ,则角位移为
,则角位移为  。
。
参考文献
|
|---|
| 线性(平动)的量 |
|
角度(转动)的量 |
| 量纲 |
— |
L |
L2 |
量纲 |
— |
— |
— |
| T |
时间: t
s |
位移积分: A
m s |
|
T |
时间: t
s |
|
|
| — |
|
距离: d, 位矢: r, s, x, 位移
m |
面积: A
m2 |
— |
|
角度: θ, 角移: θ
rad |
立體角: Ω
rad2, sr |
| T−1 |
頻率: f
s−1, Hz |
速率: v, 速度: v
m s−1 |
面積速率: ν
m2 s−1 |
T−1 |
頻率: f
s−1, Hz |
角速率: ω, 角速度: ω
rad s−1 |
|
| T−2 |
|
加速度: a
m s−2 |
|
T−2 |
|
角加速度: α
rad s−2 |
|
| T−3 |
|
加加速度: j
m s−3 |
|
T−3 |
|
角加加速度: ζ
rad s−3 |
|
|
|
| M |
质量: m
kg |
|
|
ML2 |
轉動慣量: I
kg m2 |
|
|
|---|
| MT−1 |
|
动量: p, 冲量: J
kg m s−1, N s |
作用量: 𝒮, actergy: ℵ
kg m2 s−1, J s |
ML2T−1 |
|
角动量: L, 角衝量: ι
kg m2 s−1 |
作用量: 𝒮, actergy: ℵ
kg m2 s−1, J s |
| MT−2 |
|
力: F, 重量: Fg
kg m s−2, N |
能量: E, 功: W
kg m2 s−2, J |
ML2T−2 |
|
力矩: τ, moment: M
kg m2 s−2, N m |
能量: E, 功: W
kg m2 s−2, J |
| MT−3 |
|
加力: Y
kg m s−3, N s−1 |
功率: P
kg m2 s−3, W |
ML2T−3 |
|
rotatum: P
kg m2 s−3, N m s−1 |
功率: P
kg m2 s−3, W |
|





