|
קריפטוגרפיהקריפטוגרפיה (בעברית: תּוֹרַת כְּתִיבַת הַסֵּתֶר[1]) היא ענף במתמטיקה ובמדעי המחשב העוסק במחקר ופיתוח שיטות אבטחת מידע ותקשורת נתונים על רובדיהם השונים, בסביבה פתוחה הנגישה לצד שלישי המכונה "אויב", או "יריב" פוטנציאלי. התחום מאגד תחתיו פיתוח ואנליזה של פרוטוקולים המתמודדים בהיבטים שונים של אבטחת מידע בנוכחות צד שלישי, מהם בנוסף לסודיות, הרשאת גישה, סיסמה, הוכחת ידיעה, פרוטוקול אתגר-מענה, מנגנוני חתימה דיגיטלית, חלוקת סוד, חישוב רב משתתפים בטוח, אימות זהויות, מניעת הכחשה ועוד. מערכת הצפנה משתמשת באבני בניין קריפטולוגיות כגון צופן סימטרי, צופן זרם, מפתח פומבי, פונקציות גיבוב, קוד אימות מסרים, מחולל פסבדו אקראי וכדומה. קריפטוגרפיה מודרנית משתלבת בתחומי מחקר אחרים כמו מתמטיקה, סטטיסטיקה והסתברות, תורת האינפורמציה, מדעי מחשב והנדסת אלקטרוניקה. יישומיה רבים ומגוונים וכוללים בין היתר, אבטחת רשתות תקשורת, תקשורת סלולרית, חומת אש, מסופי משיכה, כרטיסי אשראי, דואר אלקטרוני, מסחר אלקטרוני, הצבעה ממוחשבת ועוד. השם "קריפטוגרפיה" מקורו במילה היוונית "קריפטו" (κρυπτός) שמשמעותה נסתר או אומנות ההסתרה, ו"גרפיה" (γράφω) שמשמעותה "כתיבה". בתרגום חופשי נעשה שימוש בשם באופן חליפי למונח קריפטולוגיה שפירושו תורת ההסתרה (Crypto-logia, κρυπτός-λογία), אם כי משמעותו רחבה יותר מתחום ההצפנה בלבד. מונחים כלליים במובן הבסיסי, המונח הצפנה (באנגלית: encryption) מתאר הסתרת משמעותו של מסר קריא באמצעות פונקציה שמקבלת כפרמטר מפתח הצפנה והופכת את המסר לרצף של סימנים בלתי מובן לאיש. שחזור הטקסט המוצפן למצבו הקריא באמצעות פונקציה הופכית מתאימה עם מפתח הפענוח, קרוי פענוח (באנגלית: decryption). המונח צופן (Cipher) מתייחס לאלגוריתם הצפנה בדרך כלל במחשב, כאשר קלט האלגוריתם נקרא תַּמְלִיל פָּשׁוּט או טקסט גלוי (באנגלית: Plaintext) ואילו פלט האלגוריתם נקרא תַּמְלִיל מֻצְפָּן או טקסט מוצפן (באנגלית: Ciphertext). פעולת אלגוריתם ההצפנה נשלטת על ידי מפתח ההצפנה הסודי הידוע רק לשולח ולמקבל. בשפה העברית משמשת המילה צופן גם כשם עצם לכתב סתר או קוד. שיטות הסתרת מידע שאינן עושות שימוש במפתח הצפנה קרויות סטגנוגרפיה. בעבר שימש המונח קריפטוגרפיה כמעט באופן בלעדי לתיאור הצפנת מסרים. אולם בעידן המודרני התחום הלך והתרחב והוא משמש כיום לתיאור ענף מדעי רחב היקף העוסק בהיבטים השונים של אבטחת המידע, אלגוריתמים קריפטוגרפיים, פרוטוקולים ומנגנוני אבטחת מידע, פרוטקולי אימות זהויות, שיטות הבטחת שלמות ופסבדו-אקראיות. בניסוח פורמלי, משמשת המילה קריפטוגרפיה לתיאור שיטות יישום ההצפנה ואילו קריפטואנליזה מתמקדת בחקר השיטות לשבירתה. את תחום המחקר המאגד את שניהם מכנים קריפטולוגיה. בניסוח לא פורמלי, ניתן לעשות שימוש במילה קריפטוגרפיה כדי לתאר את הענף כולו. במערכת תקשורת טיפוסית כמו רשת האינטרנט הקריפטוגרפיה משתלבת יחד עם רכיבי תקשורת נוספים כמו איפנון, תיקון שגיאות ודחיסה. התרשים משמאל[2] מתאר באופן כללי את השלבים בהם עובר מידע הזורם בערוץ תקשורת מצד אחד לצד השני ואת מיקומה של הקריפטוגרפיה במערכת כזו, בדרך כלל בין שלב קידוד המידע (כגון דחיסה) לבין קידוד הערוץ (תיקון שגיאות). קריפטוגרפיה מודרנית מטפלת בשלושה נושאים עיקריים: 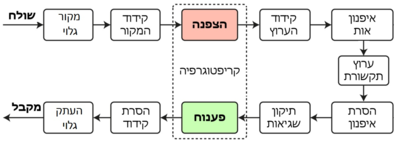
בנוסף קיימים תהליכים נלווים כגון מחולל פסאודו-אקראי המשמש בין היתר להכנת מפתחות הצפנה, פונקציות גיבוב וכדומה ותהליכים נוספים שאינם בהכרח קריפטוגרפיים. השאיפה היא שתהליכים אלו יהיו שקופים מבחינת המשתמש, כאשר משתמש מתחבר לשרת או מבצע עסקה מקוונת, ההכנות הדרושות נעשות ברקע מבלי שיחוש בכך, מלבד הדרישה מעת לעת לספק פרטי זיהוי כלשהם כמו סיסמה, מספר כרטיס וכדומה. רקע היסטורי
הצפנה ככלי לקידוד והסתרת מידע הייתה קיימת משחר ההיסטוריה. עד לעשורים האחרונים מקובל להתייחס אליה כאל הצפנה קלאסית או הצפנת 'עט ונייר'. כלומר שיטות הצפנה לקסיקוגרפיות הפועלות על סימנים כגון אותיות וספרות ומיושמות ידנית או באמצעים מכניים פרימיטיביים כמו גליל או מכונת כתיבה או בשיטות סטגנוגרפיות. התפתחותה של הקריפטוגרפיה הואצה בראשית המאה העשרים עם הופעת מנגנוני הצפנה מכניים ואלקטרו-מכניים מורכבים ומסובכים יותר ויותר, הנקראים מכונות הצפנה מבוססות רוטור, בראשן האניגמה. הקריפטוגרפיה המודרנית המוכרת לנו כיום החלה עם המצאת המחשבים, שיטות ההצפנה הפכו למתמטיות יותר ויותר באופיין ומורכבותן הפכה למסובכת מדי לביצוע באופן ידני, עד שהפכה נחלתם הבלעדית של המחשבים. במקביל התפתחה הקריפטואנליזה. מה שהחל כאמנות פיצוח קודים והמשיך עם גילוי הניתוח הסטטיסטי ככלי יעיל לשבירת צפנים. היכולת לקרוא תשדורות מוצפנות השפיע רבות על מהלך ההיסטוריה. אפשר לציין כדוגמה את מברק צימרמן שגרם להתערבותה של ארצות הברית במלחמת העולם הראשונה. או השפעת פיצוח הצפנים הנאציים בידי הבריטים, על מאזן הכוחות במלחמת העולם השנייה. בעבר שימשה הקריפטוגרפיה הקלאסית בעיקר ממשלות, צבאות, דיפלומטים ומרגלים. שני אירועים לכאורה לא קשורים שאירעו בשנות השבעים של המאה העשרים בסמיכות רבה, הביאו למפנה העיקרי ותרמו יותר מכל להפיכתה למודרנית כפי שהיא מוכרת כיום; הפצת DES כתקן הצפנה והמצאת RSA. קריפטוגרפיה מודרנית התפתחה בשני מישורים מקבילים אילו: הצפנה סימטרית והצפנה א-סימטרית. בעשורים האחרונים של המאה העשרים ההצפנה עברה מהפך משמעותי מסוג של מיומנות שהיא נחלתם של מעטים, שבעיקרה הייתה אוסף פעולות אד הוק שמסתמכות על התחכום של מפתח הצופן למדע מבוסס היטב שנשען על יסודות תאורטיים מוצקים. אפשר לחלק את הפרדיגמות המייחדות פיתוח צופן בקריפטוגרפיה המודרנית לעומת הקלאסית לשלושה צעדים עיקריים:
לצעדים אילו חשיבות הן בפיתוח הצופן כדי להבהיר מה בעצם מנסים להשיג באמצעות האלגוריתם. הן בשימוש בו, כיצד ואיפה להשתמש בו בצורה בטוחה מבלי להיכשל בשימוש לא ראוי או שימוש שלא יועד לו והן במחקר ובדיקת טיב האלגוריתם לעומת אחרים. הצפנה סימטרית
הצפנה סימטרית היא הוותיקה ביותר ושורשיה החלו עם ההצפנה הקלאסית לפני מאות שנים. הצפנה סימטרית היא אלגוריתם הצפנה שעושה שימוש באותו מפתח הן להצפנת המידע והן לפענוחו. כלומר בשיטה הסימטרית כדי שניתן יהיה להעביר מידע סודי בין הצדדים המתקשרים, שניהם נדרשים להחזיק באותו מפתח הצפנה. צופן סימטרי יכול להיות מבוסס על שתי הגישות העיקריות להצפנה סימטרית צופן זרם או צופן בלוקים כשלכל אחת מהן יתרונות וחסרונות והן מתאימות לצרכים שונים. באופן כללי יתרונותיה של ההצפנה הסימטרית הם ביעילות החישובית ובכוח המחשוב הנמוך יחסית הדרוש ליישומה לעומת הצפנה אסימטרית. למשל נכון לשנת 2015 תקן ההצפנה המתקדם נחשב לאלגוריתם הסימטרי המועדף הן מהיבט של ביטחון והן מהיבט של יעילות אף על פי שקיימים אלגוריתמים מהירים מעט יותר. ביישום ממוטב בחומרה תפוקתו היא כמעט 700 MB לשנייה לליבה אחת. התקן מגדיר מפתח הצפנה באורך של 256 סיביות כבטוח לכל צורך מעשי לתקופה הקרובה. אף על פי שקיימים אלגוריתמים סימטריים רבים, אלגוריתם DES הוא הדוגמה הקלאסית הטובה ביותר לצופן סימטרי מודרני. DES היה לאלגוריתם הסימטרי הראשון שהופץ בקנה מידה גדול ואף הפך לתקן הצפנה רשמי, שימש בעיקר בתחום הבנקאות והוא עדיין בשימוש מוגבל ב-גרסה המשולשת. אף על פי שכיום לא נחשב לאלגוריתם בטוח, חשיבותו ההיסטורית נותרה בעינה מאחר שהטכניקות שיושמו בו נלמדות כיום באקדמיה ומשמשות השראה ובסיס לאלגוריתמים סימטריים מודרניים רבים. אלגוריתמים נוספים הם 3DES, IDEA, FEAL, SAFER, RC5, RC4, Blowfish, ARIA וסרפנט. להצפנה סימטרית מספר חסרונות:
הצפנה מודרנית מטפלת בבעיות המנויות בכמה אופנים. פתרון מקובל אחד, הוא העברה בטוחה של מפתח הצפנה חד פעמי (המוצפן באמצעים אסימטריים כגון RSA) לידי המקבל יחד עם המידע המוצפן, בכך אין צורך באחסון כלל ובגמר השימוש בו המפתח יכול להיות מושמד. טכניקה נפוצה היא שילוב של שיטות סימטריות עם אסימטריות, תוך ניצול היתרונות שבכל אחת מהן להשגת בטיחות אופטימלית. קיים מגוון גדול של פרוטוקולים קריפטוגרפיים למטרות של העברה בטוחה, אימות והבטחת שלמות של מפתחות הצפנה. חלקם נשענים על שיטות סימטריות בלבד, חלקם נעזרים בסיוע צד-שלישי נאמן (TTP) וחלקם משלבים גם שיטות אסימטריות. בעוד אחרים מספקים גם אימות והוכחת זהות חד כיוונית או דו כיוונית (שרת מול לקוח ולקוח מול שרת). פרוטוקול דיפי-הלמן היה לאלגוריתם הראשון שהתמודד עם בעיית העברת המפתחות בשיטה האסימטרית. פרוטוקול זה מאפשר העברת מפתח הצפנה סימטרי בצורה מאובטחת בתשתית גלויה מבלי שהמשתתפים יאלצו להיפגש כלל. אולם אינו פותר את בעיית האימות. חתימה דיגיטלית בשילוב עם אלמנטים בסיסיים אחרים כגון מחולל אקראי בטוח, פונקציית גיבוב וכדומה, יכולים לספק הגנה כוללת ופתרון מלא לבעיות המנויות. סודיות מושלמת
בשנת 1949 הראה קלוד שאנון אבי תורת האינפורמציה[3], שיטת הצפנה (סימטרית) "מושלמת" המכונה פנקס חד-פעמי (One time pad). שיטה זו המבוססת על צופן ורנם, בה מצפינים מחרוזת מסר על ידי חיבור XOR של סיביות המסר בזו אחר זו, עם מפתח שנבחר באופן אקראי. אם המפתח אקראי "אמיתי" וחד-פעמי ובאורך המסר המיועד להצפנה, הצופן יהיה בעל סודיות מושלמת (Perfect Secrecy) והוא בטוח ללא סייג. אין שום דרך לשחזרו ללא המפתח (אפילו במקרה שמנחשים מפתח, אין דרך לדעת האם הוא המפתח הנכון). פנקס חד-פעמי מחייב שימוש יחיד במפתח. המפתח חייב להיות ממקור אקראי אמיתי (בניגוד למספרים פסבדו אקראיים המיוצרים על ידי מחשב). שיטה זו אינה מעשית ביישומים רבים משתי סיבות עיקריות: ראשית, הכנת מפתח אקראי (אמיתי) באורך המסר הופכת קשה כאשר מדובר במסר גדול מאוד. שנית, הצורך בהעברת מפתח ההצפנה הסודי לידי המקבל כרוך בסיכון רב. דרוש לשם כך ערוץ התקשרות בטוח שישמש להעברת המפתח, מה שהופך את השיטה ללא ישימה בסיטואציות רבות, בעיקר כאשר לא היה קשר מוקדם בין הצדדים המתקשרים (דוגמת מסחר ברשת האינטרנט). עם זאת, עדיין קיימים שימושים מעשיים מעטים לשיטה זו. קיימים אלגוריתמים קוונטיים המאפשרים תאורטית להתגבר על מכשול בעיית העברת המפתח, ומספקים בטיחות מוכחת. הצפנה א-סימטרית
 הצפנה סימטרית פועלת עם מפתח הצפנה זהה הן להצפנה והן לפענוח ובדרך כלל נדרש להחליפו מעת לעת. החיסרון העיקרי בשיטות הצפנה סימטריות הוא העובדה שיש לשמור את מפתח ההצפנה בסוד ואין לחשוף אותו בשום שלב לאף אחד מלבד המשתתפים הלגיטימיים, עובדה שיוצרת בעיה מהותית הנקראת בעיית הפצת מפתחות. כל זוג מתקשרים אפשרי צריכים לשתף ביניהם מפתח הצפנה סודי נפרד לצורך התקשרות אחת או מספר מוגבל של התקשרויות ולשם כך הם צריכים למצוא דרך להעבירו מאחד לשני בסודיות ולאחסנו במקום מוגן. בתקשורת מודרנית מספר המפתחות האפשריים שיש לנהל מבחינה פרקטית הופך לנטל כבד ולעיתים אינו מעשי. בעיה זו נקראת גם פרדוקס הביצה והתרנגולת כיוון שאם קיימת דרך בטוחה להעביר מפתח הצפנה סודי מלכתחילה הרי שאין צורך בהצפנה כי אפשר להשתמש בה להעברת המסר עצמו, מאידך אם אין דרך כזו כיצד יוכלו להעביר מסרים מוצפנים ביניהם ולפענח אותם אם המתקשרים מעולם לא נפגשו. במאמר מפורסם משנת 1976 "כיוונים חדשים בהצפנה"[4] הציעו ויטפילד דיפי ומרטין הלמן רעיון פורץ דרך ומהפכני לאותה עת לפתור את הבעיה באמצעות הצפנת מפתח ציבורי או באופן כללי יותר הצפנה אסימטרית. ההצפנה האסימטרית היא שיטת הצפנה שבה המקבל מכין לעצמו שני מפתחות, אחד הנקרא מפתח פרטי שנשמר בסוד ומשמש לפענוח ואילו השני נקרא מפתח ציבורי המפורסם לכל דורש ומיועד להצפנה בלבד. אף על פי שקיים קשר הדוק בין שני המפתחות למתבונן מהצד אמור להיות קשה מאוד לנחש מהו מפתח אחד בהינתן השני ולהפך. בדרך זו כל אחד יכול להצפין מידע עם המפתח הציבורי של המקבל כי הוא ידוע לכל, אך רק המקבל לבדו מסוגל לפענחו עם מפתח הפענוח המתאים שנשמר בסוד. השיטה האסימטרית מתגלה כשימושית במיוחד כאשר צד אחד רוצה להעביר לצד השני מפתח שיחה לצורך הצפנה/פענוח של מידע שהוא מעוניין לחלוק עמו. הוא עושה זאת על ידי הצפנתו באמצעות המפתח הציבורי של המקבל והמקבל מצידו יכול לפענח את המסר ולקבל את מפתח השיחה מבלי שיצטרך לשתף מידע כלשהו מראש עם השולח. עם מפתח זה שני הצדדים יכולים לבצע התקשרות מוצפנת בבטחה, באמצעות צופן סימטרי מהיר. ההיסטוריון דייוויד קאהן כינה את הצפנת המפתח הציבורי הקונספט המהפכני ביותר מאז המצאת צופן החלפה פולי-אלפביתי בתקופת הרנסאנס[5]. דיפי והלמן הוכיחו שאפשר לעשות זאת על ידי מה שנקרא מאוחר יותר פרוטוקול דיפי הלמן הנמצא עד היום בשימוש נרחב ובכך מצאו למעשה פתרון יעיל לבעיית הפצת המפתחות. בנוסף העלו השניים לראשונה את רעיון החתימה הדיגיטלית המדמה חתימה קונבנציונלית על מסמך דיגיטלי אם כי לא הציעו פתרון מעשי. המאמר של דיפי והלמן הצית את הדמיון הציבורי ועורר הדים רבים. הם ציינו במאמרם את העובדה שהרעיון שלהם שאב השראה בין היתר מרלף מרקל שעבד על רעיון משלו הנקרא חידות מרקל שלא זכה לפרסום. בעקבות פרסום המאמר ולאחר מאמצים רבים מצד האקדמיה התגלו ברבות הימים שיטות מפתח ציבורי רבות. כשנה לאחר מכן ב-1978 פיתחו עדי שמיר, רונלד ריבסט ולאונרד אדלמן את RSA שהיא שיטת מפתח ציבורי שלמה הראשונה אשר יכלה לשמש הן להצפנה והן לחתימה דיגיטלית והיא בשימוש עד ימינו. לאחריה התגלו שיטות נוספות כגון צופן אל-גמאל, הצפנת רבין, הצפנת קריימר-שופ, הצפנת תרמיל, NTRU, הצפנת מקאליס ועוד רבות. מסמך[6] שפורסם ב-1997 על ידי ממשלת בריטניה חשף כי המודיעין הבריטי (GCHQ) היה מודע כבר ב-1970 לרעיון ההצפנה האסימטרית. המתמטיקאים ג'יימס אליס וקילפורד קוקס שעבדו למען המודיעין הבריטי באותה עת פרסמו כל אחד בנפרד מאמרים בהם טענו שפיתחו שיטות דומות ל-RSA ודיפי-הלמן אך נשמרו בזמנו בסוד מטעמים של ביטחון לאומי. העובדה שקיים קשר חד-חד ערכי בין המפתח הפרטי למפתח הציבורי של המקבל מאפשרת יישום חתימה דיגיטלית המקשרת באופן חד ערכי בין תוכן מסמך דיגיטלי כלשהו לבין ערך הנקרא חתימה באופן שלא ניתן "להעביר" חתימה ממסמך אחד לאחר. המפתח הפרטי של החותם משמש לחתימה ואילו המפתח הציבורי משמש לאימות החתימה. היות שהמפתח הציבורי ידוע לכל, כל אחד יכול לאמת את החתימה אולם כדי לזייפה במטרה לשכנע אחרים שהחותם הלגיטימי ביצע את החתימה יש צורך לדעת מהו המפתח הפרטי של אותו חותם. דוגמה לאלגוריתם חתימה דיגיטלית שהפך במהרה לתקן רשמי של ממשלת ארצות הברית ומשמש בתפקיד זה עד ימינו הוא DSA. ביטחון הצפנת מפתח ציבורי מבוסס על הסיבוכיות החישובית של בעיות מתמטיות שונות הנקראות "קשות", חלקן מתורת המספרים וחלקן מתחומים מתמטיים אחרים. בעיות אילו מאפשרות הכנת פונקציה חד-כיוונית שמהווה בסיס להצפנת מפתח ציבורי. למשל הקושי בפתרון בעיית RSA והצפנת רבין מסתמך על ההנחה שקשה מאוד לפרק לגורמים מספרים שלמים גדולים. בעוד שקל לחשב העלאה בחזקה מודולרית, הרי שההפך, חישוב שורש מודולורי קשה מאוד אלא אם כן ידועים הגורמים הראשוניים. זוהי פונקציה חד-כיוונית עם "דלת צונחת" (מידע נוסף המאפשר פתרון הבעיה בזמן יעיל, במקרה זה המידע הנוסף הוא הגורמים הראשוניים). ביטחון פרוטוקול דיפי והלמן מסתמך על הקושי המשוער שבבעיית הלוגריתם הבדיד (גם היא מתורת המספרים). הצפנת NTRU היא דוגמה לאלגוריתם אסימטרי שביטחונו המסתמך על ההנחה שקשה לפתור את בעיית הווקטור הקצר ביותר בתורת הסריגים וכן הצפנת מקאליס היא דוגמה למערכת אסימטרית המבוססת על תורת הקודים. המכנה המשותף של כל המערכות האסימטריות בימינו לעומת הצפנה סימטרית, הוא היעילות החישובית. מרבית האלגוריתמים נדרשים לבצע חישובים אריתמטיים ארוכים מאוד בשל העובדה שהבעיות המתמטיות האמורות ניתנות לפתרון באמצעות אלגוריתמים המסוגלים לתת פתרון בזמן ריצה תת-מעריכי שזה טוב יותר מכוח גס כלומר ניסוי כל האפשרויות או מחצית מהן במקרה הממוצע עד לגילוי מפתח ההצפנה. כדי לפצות על כך יש צורך להגדיל את מפתחות ההצפנה בהתאם כך שסיבוכיות הניסיון לשבור את ההצפנה עם מיטב האלגוריתמים הידועים תהיה מעבר ליכולת המחשוב הנוכחית. מסיבה זו השימוש בהצפנה אסימטרית בדרך כלל מוגבל לכמות מועטה של מידע והוא משולב במערכת היברדית עם הצפנה סימטרית לניצול מיטבי של היתרונות שבשתי השיטות. בדרך כלל מפתח ציבורי משמש להעברת מפתח הצפנה סודי, כאשר את ההצפנה בפועל מעדיפים לבצע עם אלגוריתם סימטרי מהיר כמו AES. עיקרון קרקהופס
בכל מערכת הצפנה קיים מפתח שאותו יש לשמור בסוד מוחלט. גילוי המפתח על ידי צד שלישי גורם להצפנה להיכשל כיוון שעם מפתח זה היריב יכול לפענח את המידע באותה הדרך שהמקבל עושה זאת, לכן סודיות המפתח היא קריטית ביותר. השאלה שעולה היא האם כדאי להסתיר גם את אלגוריתם ההצפנה כנדבך נוסף של ביטחון. במאה ה-17 ענה על שאלה זו אוגוסטה קרקהופס במספר עקרונות צבאיים[7] שפיתח שהחשוב שבהם הוא ששיטת הצפנה אינה חייבת להיות סודית ורצוי אפילו שלא תהיה. תמיד קיימת אפשרות שתיפול לידי האויב, לכן ביטחונה אינו אמור להסתמך על סודיותה אלא אך ורק על סודיות המפתח, כך שאם אלגוריתם ההצפנה אכן יפול לידי האויב שזהו סיכון ריאלי, לא יסכן הדבר את ביטחון המידע שהוצפן, כל עוד המפתח לא נחשף. שנים מאוחר יותר ניסח שאנון מחדש את העיקרון בביטוי "האויב מכיר את המערכת שבשימוש"[8] שמהווה מוסכמה ידועה בקריפטוגרפיה. ההנחה הבסיסית בניתוח מערכת הצפנה היא שפרטי אלגוריתם ההצפנה ידועים ומפורסמים לכל, אף על פי שהנחה זו לא תמיד נכונה. יתרה מזו הרבה יותר קשה לשמר סודיות אלגוריתם הצפנה מאשר מפתח הצפנה מכמה סיבות[9]:
למרות הסיבות המשכנעות, הרעיון של קריפטוגרפיה פתוחה לפי עקרון קרקהופס לא תמיד מתקבל ואנשים נוקטים לפעמים בגישה של ביטחון באמצעות עמימות, ופעם אחר פעם לאורך ההיסטוריה רואים את ההשלכות ההרסניות של גישה זו. אלגוריתמים מוצלחים הם כאלו שזכו לביקורת ציבורית, במיוחד לעיון מדוקדק בידי אנליסטים ומומחי הצפנה מסביב לעולם. קיים מגוון עשיר של אלגוריתמים טובים שאומצו על ידי ארגוני תקינה בינלאומיים, הם חופשיים לשימוש ואינם מוגנים בפטנטים כלשהם. AES הוא דוגמה טובה לאלגוריתם שנבדק היטב על ידי מומחים רבים ונבחר מבין מספר מועמדים לאחר תחרות פתוחה שנמשכה כמה שנים. בעבר נטו מפתחי הצפנים לשמור את פרטי אלגוריתם ההצפנה בסוד. אולם גם בהצפנה המודרנית אפשר לראות מקרים שבהם אלגוריתמי הצפנה נשמרו בסוד. בשנת 1993 פרסמה ממשלת ארצות הברית תקן הצפנה בשבב Clipper שהשתמש במספר אלגוריתמים סודיים, ביניהם צופן סימטרי בשם Skipjack. השבב בין היתר נועד לאפשר לרשויות גישה לתוכן המוצפן באמצעות דלת אחורית - מפתח נוסף אותו קיבלו בעת ייצור השבב[10]. השימוש בדלת אחורית וסודיות האלגוריתמים גרמו להסתייגות רבה בציבור והפרויקט לא התקבל, במיוחד לאחר שפורסמו אלטרנטיבות טובות כמו PGP. בסופו של דבר נחשפו פרטי אלגוריתם סקיפג'ק לידיעת הציבור[11]. צופן זרם RC4 היה סוד מסחרי כשהומצא ב-1987 על ידי רונלד ריבסט במעבדות RSA. אולם בדרך כלשהי הצליח מישהו להנדס לאחור את האלגוריתם ופרטיו דלפו באופן אנונימי לרשת האינטרנט והפכו במהרה לנחלת הכלל. דוגמה אחרת היא אלגוריתם ההצפנה A5/1 ששימש בעבר בתקן GSM שהיה סודי וגרם למבוכה רבה כאשר התברר לאחר הנדסה לאחור שהוא חלש באופן משמעותי. הדעה הרווחת היא שמדינות אחדות החברות בגוש האירופי עמדו על כך שהאלגוריתם יוחלש במכוון. קריפטואנליזה
מטרת הקריפטואנליזה היא מציאת נקודות תורפה בסכמות הצפנה בפרט ובמערכות אבטחת מידע בכלל. קיימת מעין תחרות סמויה בין ממציאי האלגוריתמים לבין האנליסטים שמנתחים אותם. התפתחות הקריפטוגרפיה המודרנית נעשית בשני מסלולים מקבילים - התפתחות של שיטות הצפנה מתקדמות יותר ומאידך התפתחות שיטות פיצוח החושפות חולשות בשיטות אילו וחוזר חלילה. די בהוכחה תאורטית שאלגוריתם הצפנה ניתן לפיצוח בכמות עבודה נמוכה משמעותית מזו שהצהירו עליה מפתחי האלגוריתם או בכמות עבודה נמוכה במידה ניכרת מכוח גס כדי להוציאו מכלל שימוש. מפתחים נדרשים להתמודד עם שיטות פריצה חדשות שמתגלות והם נאלצים בעקבות כך להוציא גרסאות משופרות העמידות בפני ההתקפות שהתגלו. קריפטואנליזה של מערכת הצפנה מתחלקת לכמה מודלים מהקל אל הכבד[12]:
שתי ההתקפות הראשונות נחשבות להתקפות פאסיביות במובן שלמתקיף אין שליטה על תוכן המידע שהשיג לפני שהוא מתחיל בהתקפה או במהלכה. לעומת זאת שתי ההתקפות האחרונות נקראות אקטיביות במובן שהיריב מסוגל להתערב בנעשה ברשת לשלוח או לשנות מסרים כרצונו וכן הוא יכול באופן אדפטיבי בהתאם לתוצאות קודמות לבקש הצפנה או פענוח של כל טקסט אחר שיעלה בדעתו מלבד הטקסט המוצפן שברצונו לפצח. קל להבין ששתי ההתקפות הראשונות די מעשיות, אולם קשה להבין בשתי האחרונות כיצד מוענקת ליריב עוצמה כזו. אולם לעיתים קרובות התקפות מסוג זה אפשריות נגד מערכות הצפנה בשל העובדה שהתקשורת נעשית בין מחשבים ללא התערבות אנושית ולא תמיד המערכות מיושמות בדרך בטוחה ואילו הן הפרצות שפותחות פתח להתקפות מסוג זה. עמידות מערכת הצפנה כנגד ההתקפות המתוארות משתנה בהתאם לשיקולים רבים בהם: אופי היישום, דרישות מערכת, יעילות, מידת האיום ואילוצים אחרים כמו הצורך בתאימות. מצד אחד העדיפות היא שמערכת ההצפנה תהיה עמידה נגד המודל החזק ביותר אולם המחיר הוא ירידה בתפוקה וביעילות. לכן חשוב להעריך בדיוק רב ככל האפשר את מידת האיום ובהתאם לכך לקבוע את רמת הביטחון של המערכת. בנוסף חשוב להשוות בין רמת ביטחון של כל מרכיבי המערכת, כי ההנחה היא שהמתקיף תמיד יבחר בחוליה החלשה ביותר של המערכת להתקפה. כדי לנסח היטב הגדרת ביטחון של מערכת הצפנה יש צורך להגדיר תחילה מה הם היעדים, מה מידת האיום ומה הם המשאבים הזמינים. אפשר לתת הגדרה כללית ביותר כדלהלן:
במילה פונקציה מתכוונים באופן כללי לכך שהיריב לא יכול ללמוד דבר מהטקסט המוצפן שיכול לעזור לו לגלות משהו מועיל בנוגע לטקסט הקריא או מפתח ההצפנה. זהו הניסוח הכי קרוב להגדרת ביטחון סמנטי ובאופן כללי מספק חלקית, כי יש להביא בחשבון מספר היבטים. הגדרה יותר מדויקת צריכה להיות בסגנון: שיטת הצפנה המיועדת למשימה ספציפית תהיה בטוחה אם לא קיים יריב בעל עוצמה מוגדרת מראש שיכול להשיג שבירה של המערכת בהתאם להגדרה ביחס למשימה המוצהרת. התקפה דיפרנציאלית
פיתוח אלגוריתם הצפנה בטוח הוא משימה קשה, ומורכבותו לא בהכרח מעידה על ביטחונו. קיימות שיטות פיצוח טובות שהתפתחו במרוצת השנים שאיתן אפשר לפצח אלגוריתמים קריפטוגרפיים מסוגים שונים. בשנות ה-80 של המאה העשרים פותחה הקריפטואנליזה הדיפרנציאלית על ידי אלי ביהם ועדי שמיר. זוהי קריפטואנליזה גנרית רבת עוצמה כנגד כל סוגי הצפנים הסימטריים, היא הוכיחה את עצמה בשבירת צפנים ידועים (כמו FEAL) ומקובל כיום להתייחס אליה כאל מדד ביטחון עבור כל צופן סימטרי מודרני. התקפה דיפרנציאלית היא סוג של התקפת גלוי-נבחר הבודקת הפרשים ספציפיים בין קלט הפונקציה המובילים להפרשים ספציפיים בפלט בשיעור גבוה מן הצפוי מפרמוטציה אקראית. לדוגמה עבור בלוק באורך סיביות, אומרים שהדיפרנציאל יופיע בהסתברות , אם בהינתן קלטים אקראיים ו- באורך סיביות כל אחד, המקיימים ונתון מפתח אקראי כלשהו , ההסתברות שהדיפרנציאל של הפונקציה שלהם הוא היא . מהיבט תאורטי במקרה של פונקציה אקראית אמיתית לא אמורים להופיע דיפרנציאלים בהסתברות גבוהה מ-. אם הדיפרנציאלים של צופן בלוקים מסוים גבוהים משיעור זה באופן משמעותי הוא אינו נחשב לתמורה פסאודו-אקראית. עם דיפרנציאלים רבים כאלו המושגים אם על ידי ניתוח מדוקדק של הצופן או על ידי הכנה מוקדמת באמצעות כוח גס, אפשר לחלץ את מפתח ההצפנה. אף על פי שההתקפה יושמה לראשונה נגד DES למרבה ההפתעה לא הביאה לשבירתו. מאוחר יותר התגלה שמפתחי DES היו מודעים להתקפה הדיפרנציאלית אך שמרו זאת בסוד. הם בחרו את ערכי תיבות ההחלפה שלו בצורה כזו שיהיה עמיד נגדה. צפנים אחרים כמו FEAL לא היו בני מזל כמוהו ולא עמדו במבחן. התקפה ליניארית
קריפטואנליזה רבת עוצמה אחרת שפותחה על ידי מיצורו מצואי בראשית שנות התשעים של המאה העשרים, היא התקפה גנרית מסוג גלוי-ידוע המתמקדת ביחסים הליניאריים (או רמת המתאם) בין קלט הפונקציה לבין הפלט. למשל עבור קלט אקראי ומפתח הסיביות במיקומים עד של והמיקומים עד של הפלט של הפונקציה מכילות הטיה אם מתקיים . כאשר הוא פלט הפונקציה והפרמטרים מייצגים סיביות במיקומים ספציפיים של הקלט והפלט בהתאמה. עבור פונקציה אקראית אמיתית ההטיה הצפויה היא 0.5. אם עבור צופן סימטרי מסוים מתגלית הטיה גבוהה יותר משיעור זה אפילו במעט יביא הדבר לשבירתו המוחלטת. עדיין דרושה כמות רבה של זוגות טקסטים ידועים וטקסטים מוצפנים המתאימים להם. אורך מומלץ של מפתחות הצפנהאורך מפתח ההצפנה משפיע ישירות על סיבוכיות כל התקפה גנרית נגד אלגוריתם הצפנה, בהנחה שלא קיימת דרך מתוחכמת לשבירת האלגוריתם. באופן כללי כמעט כל אלגוריתם הצפנה ניתן לשבירה פשוט על ידי ניסוי כל המפתחות האפשריים עד שמוצאים את המפתח הנכון, שיטה זו נקראת כוח גס. מהיבט תאורטי ככל שמפתח ההצפנה גדול יותר סיבוכיות התקפת כוח גס עולה באופן מעריכי, אך בד בבד נפגעת יעילות האלגוריתם כי נדרש זמן ארוך יותר לביצוע ההצפנה. על כן חשוב למצוא את האיזון בין יעילות לבין ביטחון במונחים של אורך המפתח. לשאלה מה אורך המפתחות המומלץ אין תשובה חד משמעית כיוון שהדבר תלוי בגורמים רבים, ביניהם; בסיס תאורטי, פריצות דרך מתמטיות, איכות יישום האלגוריתם, יכולת טכנולוגית נוכחית או עוצמת המחשוב של היריב או האויב וכדומה. ככלל, נכון לשנת 2017 השאיפה היא להגיע לרמת ביטחון מינימלית של , כלומר שיכולת היריב לשבור את המערכת עם מיטב האלגוריתמים הקיימים תהיה בסיבוכיות של פעולות בסיסיות בקרוב, או לחלופין, סיכוייו לשבור את האלגוריתם הם בהסתברות של . שזה נחשב בעיני רבים למרווח ביטחון מספק מהיבט מעשי בהתאם ליכולת הטכנולוגית הנוכחית. במקרה של הצפנת מפתח ציבורי כיוון שקיימים אלגוריתמים הטובים בהרבה מכוח גס הדברים שונים. עד שנת 2003 בערך, מקובל היה להשתמש במספרים באורך 1024 סיביות. מעבדות RSA פרסמו ב-2003 הצהרה לפיה מפתח אסימטרי בגודל 1024 סיביות מספק רמת הגנה מקבילה למפתח סימטרי בגודל 80 סיביות. 2048 סיביות מקבילות לאלגוריתם סימטרי עם מפתח 112 סיביות ו-3072 מקביל ל-128. המלצה שלהם להשתמש במפתח 2048 סיביות לשימוש רגיל ו-3072 סיביות לשימוש מיוחד במקרים קיצוניים, זאת עד לשנת 2030. ארגון התקינה האמריקאי נוקט בגישה מחמירה יותר, לפי תקן NIST SP 800-57 נכון ליולי 2012 מפתח אסימטרי בגודל 3072 סיביות מקביל למפתח סימטרי בגודל 128 סיביות (מהסוג הנפוץ כיום באלגוריתם AES) ואילו לרמת בטיחות גבוהה, מפתח בגודל 15,360 סיביות יתאים ברמתו למפתח סימטרי בגודל 256 סיביות. הדברים אמורים לגבי כל סוגי ההצפנה האסימטרית כולל חתימה דיגיטלית כגון DSA המבוססת על בעיית הלוגריתם הבדיד, זאת בשל ההערכה כי בעיית לוגריתם בדיד דומה בקושיה לבעיית פירוק לגורמים. יוצא מן הכלל הוא מערכת ההצפנה בעקום אליפטי (ECC). תקן FIPS PUB 186-4 שנכלל ב-Suite B של NSA, ממליץ על מפתח בגודל 256–384 סיביות שמקביל ברמתו למפתח סימטרי 128 סיביות, להצפנת מסמכים עבור הממשל האמריקאי ברמה של SECRET. לרמה של TOP SECRET ממליץ על 512 סיביות ומעלה. באופן כללי ההנחיה של NIST היא שמפתח ECC יהיה בערך כפול בגודלו ממפתח סימטרי. הערכה זו מניחה כי לא ידועה פריצת דרך משמעותית לפתרון הבעיה המתמטית עליה מבוססת ECC זאת כיוון שהאלגוריתמים הידועים אינם ישימים במערכת כזו. פרימיטיבים קריפטוגרפייםפרימיטיב קריפטוגרפי הוא הגדרה לאלגוריתם קריפטוגרפי שייעודו ספציפי למטרה או יעד מוגדר. אלגוריתם AES הוא פרימיטיב קריפטוגרפי שתפקידו להצפין מידע בשיטה סימטרית. פרימיטיבים אחרים הם RSA, פונקציית גיבוב SHA-1 וכן DSA. מהות הרעיון הוא שבהקמת מערכת אבטחת מידע שלמה, אין די באלגוריתם אחד דהיינו בפרימיטיב קריפטוגרפי אחד, אלא משלבים מספר אלגוריתמים שלכל אחד מהם תפקיד אחר. יחדיו הם משלימים זה את זה למערכת שלמה. על כן נודעת חשיבות רבה לבדיקת המאפיינים והיחסים שבין הפרימיטיבים השונים, על מנת לוודא כי השילוב ביניהם בטוח ואינו מכיל פרצות. לעיתים אי-הבנה באשר למהות פרימיטיב מסוים והניסיון לשלבו במערכת או להשתמש בו באופן שלא יועד לו, עשוי לפגוע בבטיחות המערכת כולה. לדוגמה פונקציית גיבוב טובה ליצירת ערכים ייחודיים, אולם אינה טובה כשלעצמה לצורך הצפנה. יתרונה הברור בא לידי ביטוי במערכת הצפנה דוגמת PGP בה יש צורך בערך חד-כיווני של המידע המשמש תווית לצורך החתימה על המסר באמצעות חתימה דיגיטלית. פרוטוקולים ומנגנונים קריפטוגרפיים
מערכת הצפנה שלמה היא מערכת קריפטוגרפית המשלבת מספר פרימיטיבים קריפטוגרפיים, המספקים כל אחד מהם תכונות יסודיות הקשורות באבטחת מידע כמו סודיות, אימות או הבטחת שלמות, יחד הם משלימים זה את זה למערכת שלמה שלה מספר יעד אבטחה מוגדר בהתאם לסביבה בה היא פועלת מחד ודרישות הלקוח מאידך. לעיתים מתייחסים בטעות לאלגוריתם כמערכת הצפנה אף על פי שאינו כזה. למשל RSA נקרא לפעמים מערכת הצפנה אף על פי שאסור להשתמש בו לבדו להצפנה כי ההצפנה לא תהיה בטחה כלל במקרה כזה. פרימיטיבם קריפטוגרפיים מיועדים לתת מענה ספציפי, במקרה זה יכולת א-סימטרית שטובה במיוחד להעברת מפתח הצפנה ומספקת ביטחון סמנטי נגד התקפת מוצפן-נבחר במסגרת מודל ביטחון כלשהו כמו מודל אורקל אקראי. לפעמים המערכת אמורה לספק ביטחון לאורך זמן של שירותי גיבוי ואחסון מידע ולפעמים המערכת כוללת התקשרות דו כיוונית בין שרת ולקוח או בין מספר משתתפים במקרה זה היא תקרא פרוטוקול קריפטוגרפי. דוגמאות למערכת הצפנה הן RSA, אל-גמאל או חלוקת סוד ואפס ידיעה וכדומה. דוגמאות לפרוטוקול קריפטוגרפי הן: TLS, PGP, קרברוס, ארנק אלקטרוני ו-GSM. ביטחון מערכת קריפטוגרפית או פרוטוקול קריפטוגרפי תלוי במאפייני הביטחון של הפרימיטיבים המרכיבים אותו. אך אין בזה הוכחה שהמערכת חזקה כמו סך כל המרכיבים אותה. בעבר מאפייני הביטחון של מערכת הצפנה נבדקו באופן אמפירי באמצעות שיטות אד הוק וללא בסיס תאורטי מוצק. כיום נעשים מאמצים לפתח טכניקות פורמליות לניתוח והערכת ביטחון של מערכת או פרוטוקול קריפטוגרפיים. גישה זו נקראת ביטחון מוכח, כלומר מנסים להוכיח שהמערכת בטוחה תחת מודל תאורטי כלשהו כמו מודל סיבוכיות חישובית או מודל אורקל אקראי. קריפטוגרפיה ותורת הקוונטיםבמהלך המאה ה-20 החל להתפתח בקצב מהיר ענף החישוביות הקוונטית, שעלולות להיות לו השלכות קריטיות על הקריפטוגרפיה המודרנית. אם ניתן יהיה לבנות מחשב קוונטי בעל יכולת גידול (סקאלבילי), אזי למעשה מרבית האלגוריתמים האסימטריים כגון RSA ודומיו יצאו מכלל שימוש. יהיה צורך בשדרוג מקיף של כל מערכות ההצפנה. זאת בשל קיומם של אלגוריתמים קוונטיים שמאפשרים פיצוח צפנים אילו בזמן פולינומי, לאור היכולת לבצע חישובים בצורה מהירה יותר מאשר במחשב "רגיל". הרעיון שבבסיס החישוביות הקוונטית הועלה לראשונה על ידי הפיזיקאי ריצ'רד פיינמן, שמסתמך על עקרון השזירה הקוונטית: אם מספר גדול מאוד של קיוביטים שזורים זה בזה, אזי חישובים על ביטים אלו מקבילים לביצוע חישובים רבים בו זמנית. רעיון זה קרם עור וגידים כאשר פותחו מספר אלגוריתמים קוונטיים שדורשים זמן ריצה קטן יותר מאשר מקבילם הקלסי. שני האלגוריתמים הבולטים בנושא זה הם אלגוריתם שור לפירוק לגורמים של מספר שלם שעל מחשב קוונטי מתבצע בזמן פולינומי ולא מעריכי, ואלגוריתם גרובר לחיפוש במערך לא ממוין, המתבצע בסיבוכיות זמן שהיא שורש ריבועי של הזמן הנדרש בחישוב קלאסי. אלגוריתם שור פירושו שאם אכן ייבנה מחשב קוונטי אזי ביכולתו לפרוץ מערכות הצפנה פומביות (בהן הסוד הוא פירוק לגורמים של מספר גדול). משמעות אלגוריתם גרובר היא שניתן לקצר באופן משמעותי את זמן מציאת המפתח בשיטת כוח גס. מכאן החל העיסוק בניסיון למצוא פרימיטיבים קריפטוגרפיים שנקראים פוסט קוונטיים כלומר שיהיו עמידים גם בפני מערכות חישוב קוונטיות, דוגמת הצפנה מבוססת סריג. טרם נמצאה דרך מעשית לבניית מחשבים בעלי מספר רב מאוד של ביטים קוונטיים (מחשבים סקאלאבילים), ולכן שימוש במחשבים קוונטים לפריצת מערכות הצפנה מודרניות הוא בגדר בלתי אפשרי בטכנולוגיה הקוונטית הנוכחית. הצפנה קוונטית
על פי תורת הקוונטים, ובפרט על פי עקרון אי הוודאות של הייזנברג, לא ניתן לבצע 'מדידה' מבלי להשפיע על המצב של האובייקט הנמדד. המשמעות של עיקרון זה היא שאדם המאזין לשיחה, בהכרח משפיע עליה, ומכאן שניתן לזהות את ההאזנה. בעיקרון זה נעשה שימוש להעברת מידע בצורה לגמרי מאובטחת - המזהה כל ניסיון להאזין למידע. בשנת 1984 פותח פרוטוקול ראשון המיישם עיקרון זה על-מנת לבצע החלפת מפתחות קוונטית (QKD) באופן בטוח, ולאחריו פותחו מספר פרוטוקולים נוספים אשר עושים שימוש בשיטות שונות, דוגמת שימוש במצבי EPR. ניתן לראות בפרוטוקולים אלו את המקביל הקוונטי של פרוטוקול דיפי-הלמן. בפרוטוקולים אלו הסודיות המתקבלת היא "מושלמת" במובן תורת האינפורמציה. כל ניסיון של גורם זר להתערב בפרוטוקול מסתיים בגילויה של התקיפה. אם לא נתגלתה תקיפה, מוכח כי כמות האינפורמציה שזלגה אל גורם שלישי היא זניחה. חוקיות וזכויות שימושמטבע הדברים, סגולותיה של הקריפטוגרפיה, ככלי לשמירה על פרטיות, מנוצלות לרעה על ידי גורמים זדוניים כמו ארגוני פשע, טרור וריגול. מאז ומתמיד ממשלות וגורמי ביטחון במדינות שונות גילו עניין רב בהתפתחויות בתחום זה. בכל מדינה כמעט קיים גוף האחראי על השימוש בהצפנה, מחקר ופיתוח וכן ניטור וניתוח של חומרים מוצפנים שקיים חשש שהם מסכנים את ביטחונה הלאומי. גם ארגוני זכויות האדם ברחבי העולם מגלים עניין בתחום זה בשל תרומתו לשמירת הפרטיות. בשל כך היו בעבר בארצות הברית מספר אירועים שערורייתיים, הקשורים בנושאים חוקתיים בתחום זה. ישנן מדינות (בהן ישראל) שבהן עד היום קיימות מגבלות חוקיות לעיסוק בקריפטוגרפיה ובכל מה שקשור אליה. בישראל קיים החל מ-1974 "צו צופן"[13] המחייב כל גורם המעוניין לעסוק בהצפנה בקבלת רישיון עיסוק בהצפנה ממנכ"ל משרד הביטחון (בעבר מקצין קשר ראשי בצה"ל). במדינות אחרות (כמו ארצות הברית), העיסוק בקריפטוגרפיה לא מוגבל מקומית אך קיימות מגבלות ייצוא של חומרים קריפטוגרפיים מחוץ לתחומי המדינה. למעשה בארצות הברית קריפטוגרפיה סווגה כסוג של "תחמושת" בדומה לטנק או טיל בליסטי, ובעבר אף נאסר שימוש בהצפנה חזקה בארצות הברית, כאשר הפיקוח על ההצפנה היה באחריות הסוכנות לביטחון לאומי (NSA) של ארצות הברית. NSA הוא הארגון הממשלתי הגדול והמצויד ביותר בעולם שעוסק בקריפטוגרפיה ומעסיק עשרות אלפי עובדים. מטרתו העיקרית ניטור, פענוח וחשיפת תשדורות או מידע דיגיטלי אחר ברחבי העולם, שלהם זיקה לביטחונה הלאומי של ארצות הברית. מדינות אחרות (בעיקר מדינות אירופיות) נוקטות בגישה יותר ליברלית בכל הקשור להצפנה. על אלגוריתמים קריפטוגרפיים אפשר להגן (במדינות מסוימות, כגון ארצות הברית) בפטנטים. על המימוש שלהם אפשר להגן בזכויות יוצרים (אולם אם המפרט מפורסם, כל אחד יכול לממש אותם מחדש). אפשר לנסות גם לשמור אותם כסוד מסחרי. בארצות הברית, בקנדה ובמדינות רבות אחרות רשומים מאות פטנטים על סוגים שונים של אלגוריתמים קריפטוגרפיים. לדוגמה אלגוריתם RSA נרשם כפטנט שתוקפו פג בשנת 2000. בשל המגבלה שנוצרה מהפטנט נאלצה ממשלת ארצות הברית ליצור תקן חתימה אלקטרונית חלופי בשם DSA שלא מוגן בפטנטים[14]. אי הבהירות סביב הפטנטים שעל ההצפנה בעקומים אליפטיים (ר' בהמשך) היא אחת הסיבות לחוסר הפופולריות שלהם[דרוש מקור]. בארצות הברית (וגם בישראל) רשומים מספר פטנטים על אלגוריתמים שונים להצפנה. החברה האמריקאית RSA מחזיקה כיום במספר פטנטים הקשורים לאלגוריתמי הצפנה שונים[15][דרוש מקור]. אף ששם החברה הוא "RSA", הפטנטים שבבעלותה כיום אינם בהכרח קשורים לאלגוריתם המקורי. החברה הקנדית Certicom מחזיקה בכמאה ועשרים פטנטים בהיבטים שונים של ECC (הצפנת עקום אליפטי) בארצות הברית ובקנדה בלבד. החל מאמצע שנות ה-90 של המאה העשרים היו כמה תחרויות של ממשלות לבחירת פרימיטיבים קריפטוגרפיים חדשים: תחרות AES של מכון התקנים האמריקאי[16], NESSIE של האיחוד האירופי[17], CRYPTEC ביפן[18]. בכל המקרים הללו אחד מהתנאים היה שהזוכים ישיקו את התוכנה ללא מגבלות שימוש כלשהן. אזכורים בספרות
ראו גם
לקריאה נוספת
קישורים חיצוניים
הערות שוליים
|
||||||
















![{\displaystyle \Pr[x_{i_{1}}\oplus \cdots \oplus x_{i_{\ell }}\oplus \cdots \oplus y_{i'_{\ell }}=0]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a31817f2340b71af550b4d4b3c5ab7080733dfb)




